Ax 0 where B Find a vector x not equal to 0 that holds thi

Ax = 0 where

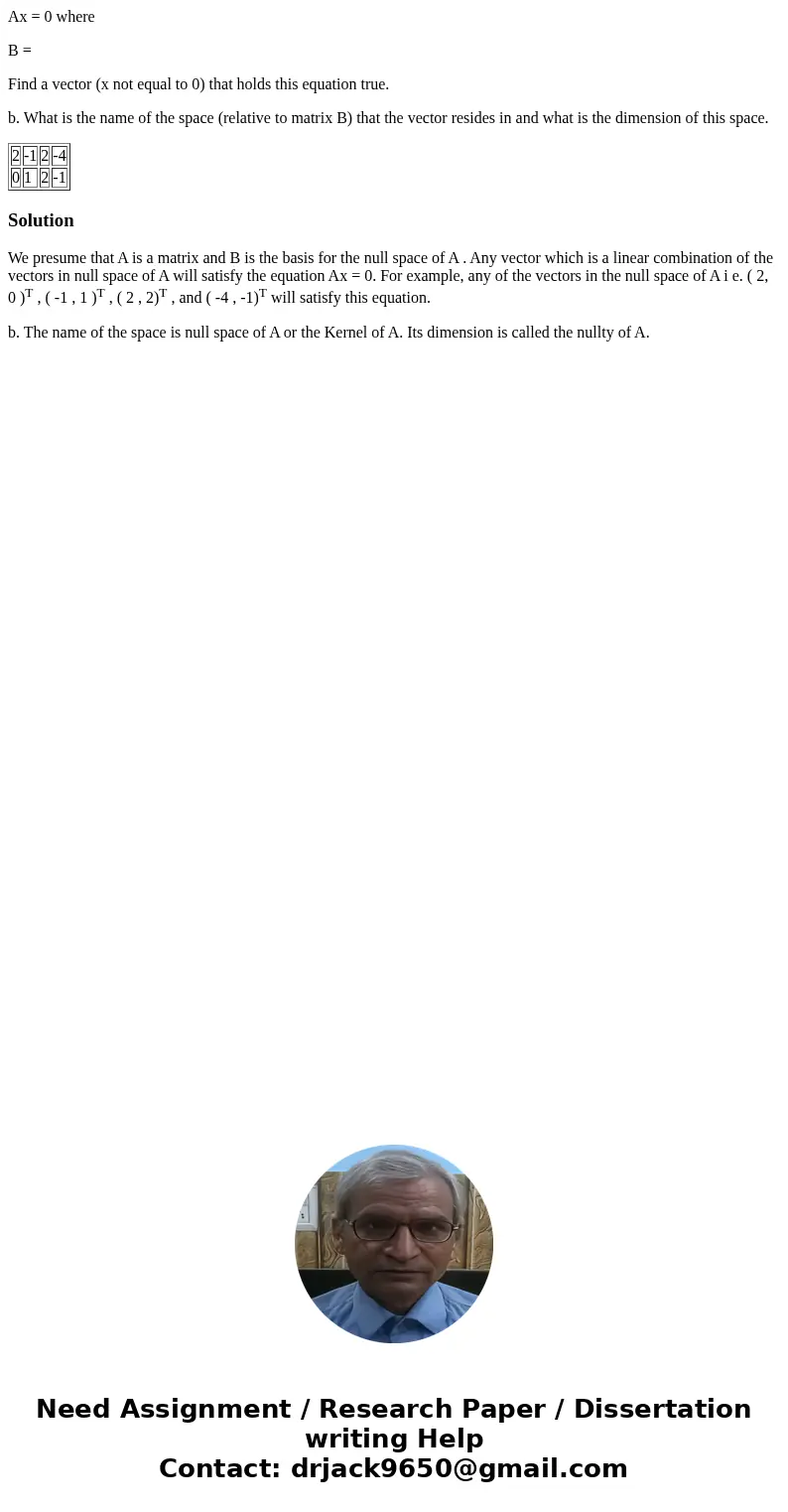
B =

Find a vector (x not equal to 0) that holds this equation true.

b. What is the name of the space (relative to matrix B) that the vector resides in and what is the dimension of this space.

Solution

We presume that A is a matrix and B is the basis for the null space of A . Any vector which is a linear combination of the vectors in null space of A will satisfy the equation Ax = 0. For example, any of the vectors in the null space of A i e. ( 2, 0 )^T , ( -1 , 1 )^T , ( 2 , 2)^T , and ( -4 , -1)^T will satisfy this equation.

b. The name of the space is null space of A or the Kernel of A. Its dimension is called the nullty of A.