Consider the sequence defined recursively by a1 2 a2 2 an

Consider the sequence defined recursively by a_1 = - 2 a_2 = -2. a_n=1 = -7a_n_1 - 8_an. We can use matrix diagonalization to find an explicit formula foran. Find a matrix that satisfies Find the appropriate exponent k such that Find a diagonal matrix D and an invertible matrix P such that M = PDP You can find an explicit formula for a_n using part b. and a formula for M^k = PD^kP 1. Try to develop this formula. Use your formula to verify the answer for part f.

Solution

Post one more question to get the remaining answers

a) an = an

a(n+1) = -7a(n-1) - 8an

Hence the matrix M will be

b) n = k + 1

k = (n-1)

Hence we need to keep k = (n-1) in order to convert an and an+1 into a1 and a2

c)

The diagonal matrix will be

The matrix P will be

d)

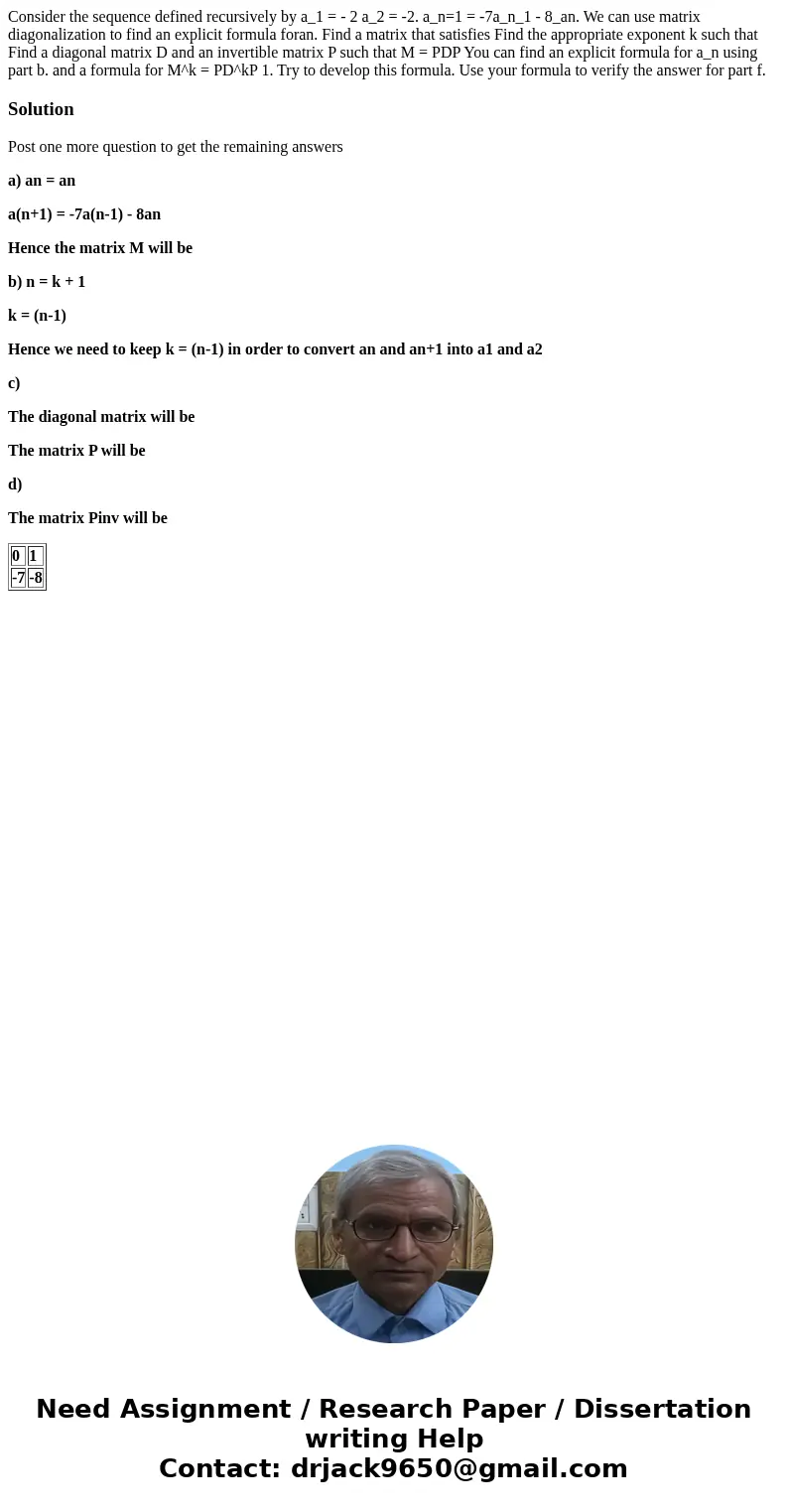
The matrix Pinv will be

0	1
-7	-8