Here is a copy of the OK WTI Spot Price FOB Dollars per Barr
Here is a copy of the “OK WTI Spot Price FOB (Dollars per Barrel)”. JUST PART C
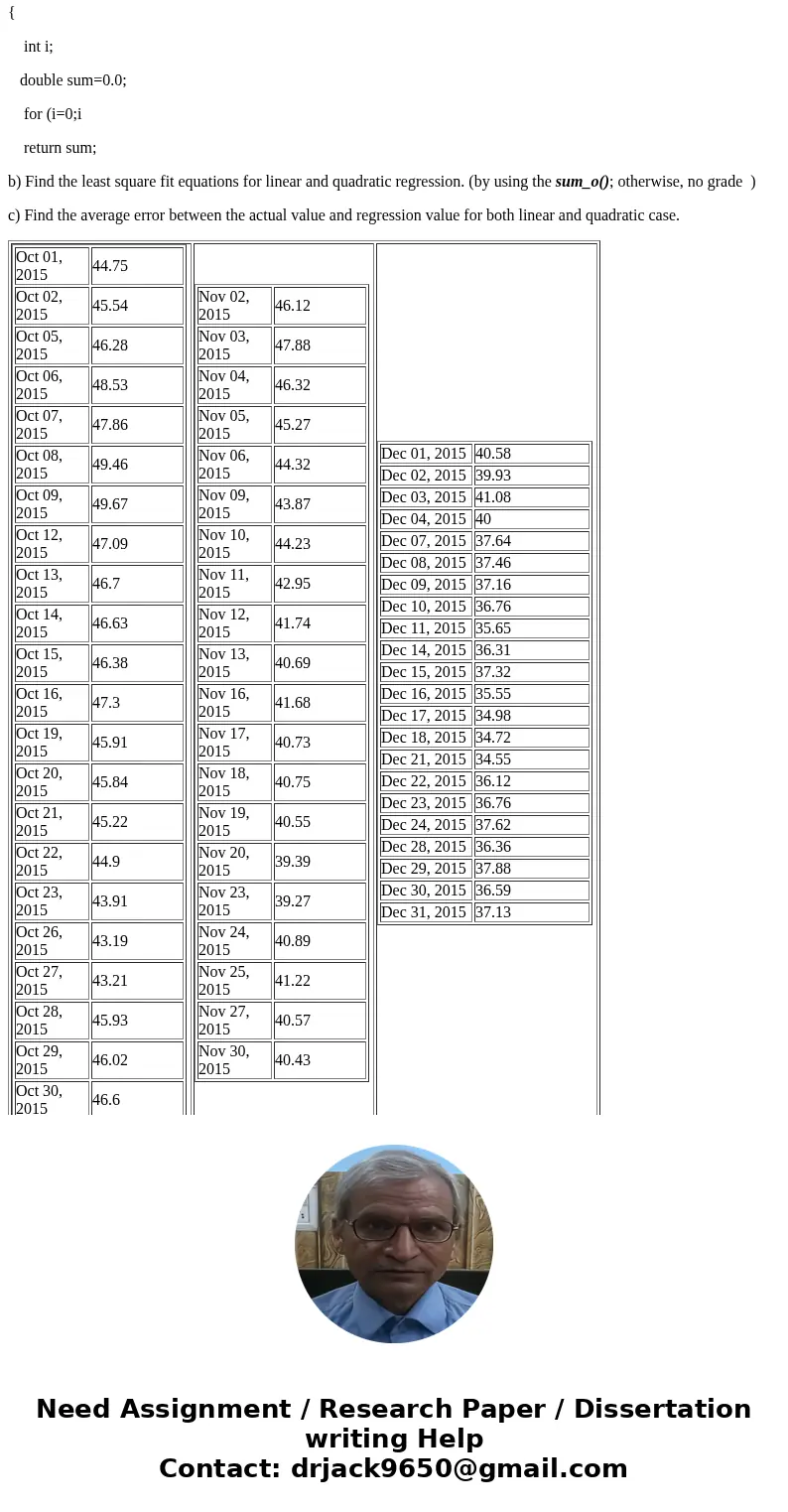
Oct 01, 2015
44.75
Oct 02, 2015
45.54
Oct 05, 2015
46.28
Oct 06, 2015
48.53
Oct 07, 2015
47.86
Oct 08, 2015
49.46
Oct 09, 2015
49.67
Oct 12, 2015
47.09
Oct 13, 2015
46.7
Oct 14, 2015
46.63
Oct 15, 2015
46.38
Oct 16, 2015
47.3
Oct 19, 2015
45.91
Oct 20, 2015
45.84
Oct 21, 2015
45.22
Oct 22, 2015
44.9
Oct 23, 2015
43.91
Oct 26, 2015
43.19
Oct 27, 2015
43.21
Oct 28, 2015
45.93
Oct 29, 2015
46.02
Oct 30, 2015
46.6
Nov 02, 2015
46.12
Nov 03, 2015
47.88
Nov 04, 2015
46.32
Nov 05, 2015
45.27
Nov 06, 2015
44.32
Nov 09, 2015
43.87
Nov 10, 2015
44.23
Nov 11, 2015
42.95
Nov 12, 2015
41.74
Nov 13, 2015
40.69
Nov 16, 2015
41.68
Nov 17, 2015
40.73
Nov 18, 2015
40.75
Nov 19, 2015
40.55
Nov 20, 2015
39.39
Nov 23, 2015
39.27
Nov 24, 2015
40.89
Nov 25, 2015
41.22
Nov 27, 2015
40.57
Nov 30, 2015
40.43
Dec 01, 2015
40.58
Dec 02, 2015
39.93
Dec 03, 2015
41.08
Dec 04, 2015
40
Dec 07, 2015
37.64
Dec 08, 2015
37.46
Dec 09, 2015
37.16
Dec 10, 2015
36.76
Dec 11, 2015
35.65
Dec 14, 2015
36.31
Dec 15, 2015
37.32
Dec 16, 2015
35.55
Dec 17, 2015
34.98
Dec 18, 2015
34.72
Dec 21, 2015
34.55
Dec 22, 2015
36.12
Dec 23, 2015
36.76
Dec 24, 2015
37.62
Dec 28, 2015
36.36
Dec 29, 2015
37.88
Dec 30, 2015
36.59
Dec 31, 2015
37.13
a) Write a C program dose the following
Use the function following
double sum_o(double *x, double *y, int n, int j, int k)
{
int i;
double sum=0.0;
for (i=0;i
return sum;
b) Find the least square fit equations for linear and quadratic regression. (by using the sum_o(); otherwise, no grade )
c) Find the average error between the actual value and regression value for both linear and quadratic case.
|
|
|
Solution
Sorts OF CONFIDENCE INTERVALS
In relapse anticipating, you might be worried with point appraisals and certainty interims for a few or the majority of the accompanying:
The coefficients of the free factors
The mean of the needy variable (i.e., the genuine area of the relapse line) for given estimations of the autonomous factors
The expectation of the needy variable for given estimations of the free factors
In all cases, there is a straightforward relationship between the point gauge and its encompassing certainty interim:
(Certainty Interval) = (Point Estimate) + (Critical t-esteem) x (Standard Deviation or Standard Error)
For a 95% certainty interim, the \"basic t esteem\" is the esteem that is surpassed with likelihood 0.025 (one-followed) in a t dissemination with n-p degrees of opportunity, where p is the quantity of coefficients in the model- - including the consistent term assuming any. (When all is said in done, for a 100*(1-x) percent certainty interim, you would utilize the t esteem surpassed with likelihood x/2.) If the quantity of degrees of flexibility is huge - say, more than 30- - the t dissemination nearly takes after the standard ordinary dispersion, and the significant basic t esteem for a 95% certainty interim is around equivalent to 2. (All the more definitely, it is 1.96.) For this situation, hence, the 95% certainty interim is generally equivalent to the point appraise \"give or take two standard deviations.\" Here is a choice of basic t qualities to use for various certainty interims and diverse quantities of degrees of flexibility, taken from a standard table of the t conveyance:
Degrees of t-esteem for certainty interim
Flexibility (n-p) half 80% 90% 95%
- - -
10 0.700 1.372 1.812 2.228
20 0.687 1.325 1.725 2.086
30 0.683 1.310 1.697 2.042
60 0.679 1.296 1.671 2.000
Interminable 0.674 1.282 1.645 1.960
A t-dispersion with \"unbounded\" degrees of opportunity is a standard typical dissemination.
The \"standard mistake\" or \"standard deviation\" in the above condition relies on upon the way of the thing for which you are processing the certainty interim. For the certainty interim around a coefficient gauge, this is basically the \"standard blunder of the coefficient appraise\" that shows up irrelevant gauge in the coefficient table. (Review this is corresponding to the standard mistake of the relapse, and conversely corresponding to the standard deviation of the autonomous variable.)
For a certainty interim for the mean (i.e., the genuine tallness of the relapse line), the pertinent standard deviation is alluded to as the \"standard deviation of the signify\" by then. This amount relies on upon the accompanying components:
The standard blunder of the relapse
the standard blunders of all the coefficient gauges
the relationship lattice of the coefficient gauges
the estimations of the free factors by then
Different things being equivalent, the standard deviation of the mean- - and thus the width of the certainty interim around the relapse line- - increments with the standard mistakes of the coefficient gauges, increments with the separations of the autonomous factors from their particular means, and declines with the level of connection between\'s the coefficient gauges. Notwithstanding, in a model described by \"multicollinearity\", the standard mistakes of the coefficients and
For a certainty interim around an expectation in light of the relapse line sooner or later, the important standard deviation is known as the \"standard deviation of the forecast.\" It mirrors the mistake in the assessed tallness of the relapse line in addition to the genuine blunder, or \"clamor,\" that is theorized in the fundamental model:
Information = SIGNAL + NOISE
For this situation, the relapse line speaks to your best gauge of the genuine flag, and the standard blunder of the relapse is your best gauge of the standard deviation of the genuine clamor. Presently (believe me), for basically the same reason that the fitted qualities are uncorrelated with the residuals, it is likewise genuine that the mistakes in evaluating the stature of the relapse line are uncorrelated with the genuine blunders. Along these lines, the fluctuations of these two parts of blunder in every forecast are added substance. Since changes are the squares of standard deviations, this implies:
(Standard deviation of prediction)^2 = (Standard deviation of mean)^2 + (Standard blunder of regression)^2
Take note of that, though the standard mistake of the relapse is a settled number, the standard deviations of the expectations and the standard deviations of the methods will more often than not shift from indicate point in time, since they rely on upon the estimations of the autonomous factors. Be that as it may, the standard blunder of the relapse is commonly much bigger than the standard mistakes of the methods at most focuses, henceforth the standard deviations of the expectations will regularly not change by much from indicate point, and will be just marginally bigger than the standard mistake of the relapse.
It is conceivable to process certainty interims for either means or expectations around the fitted qualities and/or around any genuine conjectures which may have been created. Statgraphics and RegressIt will consequently produce gauges as opposed to fitted values wherever the reliant variable is \"missing\" yet the autonomous factors are definitely not. Certainty interims for the gauges are likewise reported. Here is a case of a plot of estimates with certainty limits for means and conjectures created by RegressIt for the relapse show fitted to the characteristic log of instances of 18-packs sold. On the off chance that you look carefully, you will see that the certainty interims for means (spoke to by the internal arrangement of bars around the point conjectures) are observably more extensive for amazingly high or low estimations of cost, while the certainty interims for figures are most certainly not.






 Homework Sourse
Homework Sourse