answer in back is 205m just cant figure out how to get there

answer in back is 20.5m just cant figure out how to get there

The force F, acting in a constant direction on the 20-kg block, has a magnitude which varies with the position s of the block. Determine how far the block must slide before its velocity becomes 15 m/s. When s = 0 the block is moving to the right at v = 6 m/s. The coefficient of kinetic friction between the block and surface is mu_k = 0.3.

Solution

Net force acting on the block

Fn = 50s^1/2 – 0.3*20*9.8

        = 50s^1/2 – 58.8

acceleration a = F/m = 2.5s^1/2 - 2.94

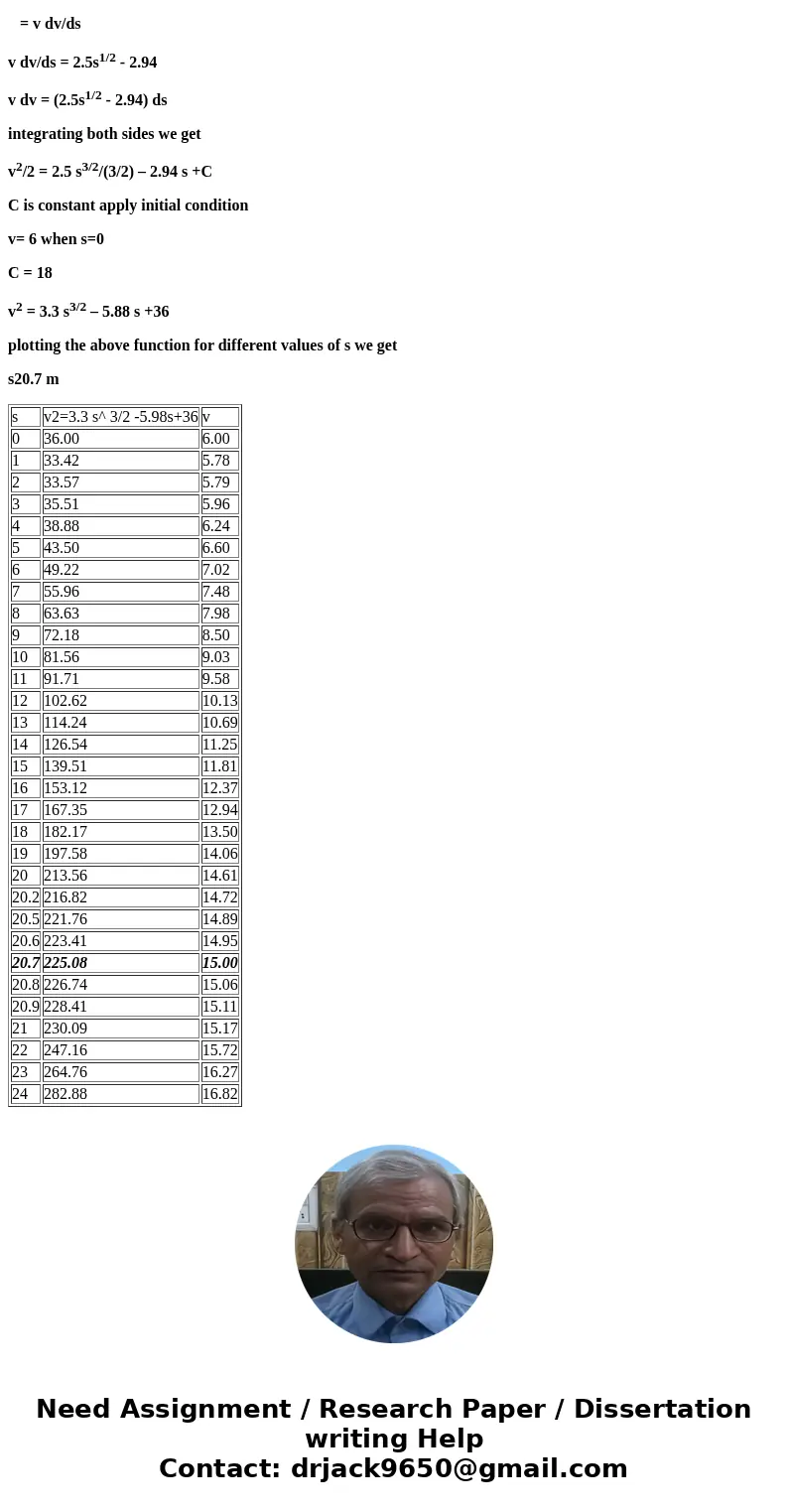
a = dv/dt = dv/ds *ds/dt

   = v dv/ds

v dv/ds = 2.5s^1/2 - 2.94

v dv = (2.5s^1/2 - 2.94) ds

integrating both sides we get

v²/2 = 2.5 s^3/2/(3/2) – 2.94 s +C

C is constant apply initial condition

v= 6 when s=0

C = 18

v² = 3.3 s^3/2 – 5.88 s +36

plotting the above function for different values of s we get

s20.7 m

s	v2=3.3 s^ 3/2 -5.98s+36	v
0	36.00	6.00
1	33.42	5.78
2	33.57	5.79
3	35.51	5.96
4	38.88	6.24
5	43.50	6.60
6	49.22	7.02
7	55.96	7.48
8	63.63	7.98
9	72.18	8.50
10	81.56	9.03
11	91.71	9.58
12	102.62	10.13
13	114.24	10.69
14	126.54	11.25
15	139.51	11.81
16	153.12	12.37
17	167.35	12.94
18	182.17	13.50
19	197.58	14.06
20	213.56	14.61
20.2	216.82	14.72
20.5	221.76	14.89
20.6	223.41	14.95
20.7	225.08	15.00
20.8	226.74	15.06
20.9	228.41	15.11
21	230.09	15.17
22	247.16	15.72
23	264.76	16.27
24	282.88	16.82