Using the algorithm Find an LCS of x and y using the algor

Using the algorithm:

Find an LCS of x = and y = using the algorithm learned in class Show the c and b table write the LCS and the LCS length based on the results in your tables using algorithm: LCS-LENGTH(X Y) m = X. length n = Y. length let b[1..m, 1..n] and c[0..m, 0..n] be new tables for i = 1 to m c[i, 0] = 0 for j = 0to n c[0, j] = 0 for i = 1 to n if x_i == y_j c[I, j] = c[i - 1, j - 1] + 1 b[I, j] = \"left arrow\" elseif c[i - 1, j] greaterthanorequalto c[i, j - 1] c[I, j] = c[i - 1, j] b[I, j] = \"up arrow\" else c[I, j] = c[I, j - 1] b[I, j] = \"left arrow\" return c and b

Solution

LCS = { 2, 3, 1, 0 }

length of LCS = 4

B : Rows represent increment in index of X array, columns represent increment in Y

C :   d means left-right diagonal arrow,   l mean left arrow, u mean upper arrow

- means, value is not stored by algo, hence garbage

Following is c++ code used, just in case:

#include <iostream>
using namespace std;

void lcs( int* x, int* y, int m, int n ){
   char b[m][n];
   int c[m][n];
   for(int i = 1 ; i < m; i++){ c[i][0] = 0; }
   for(int i = 0; i < n; i++){ c[0][i] = 0; }
   for(int i = 1; i < m; i++){
       for(int j = 1; j < n; j++){
           if( x[i] == y[j] ){
               c[i][j] = c[i-1][j-1] + 1;
               b[i][j] = \'d\';
           }
           else if( c[i-1][j] >= c[i][j-1] ){
               c[i][j] = c[i-1][j];
               b[i][j] = \'u\';
           }
           else{
               c[i][j] = c[i][j-1];
               b[i][j] = \'l\';
           }
       }
   }

   for(int i = 0; i < m; i++){
       for(int j = 0; j < n; j++){
           cout << c[i][j] << \" \"; } cout << endl; }

           cout << endl;
   for(int i = 0; i < m; i++){
       for(int j = 0; j < n; j++){
           cout << b[i][j] << \" \"; } cout << endl; }
  
}

int main(){

   int x[] = {3,2,3,1,0,2};
   int y[] = {1,2,1,0,3,1,0,3};
   lcs( x, y, sizeof(x)/sizeof(x[0]), sizeof(y)/sizeof(y[0] ) );
}

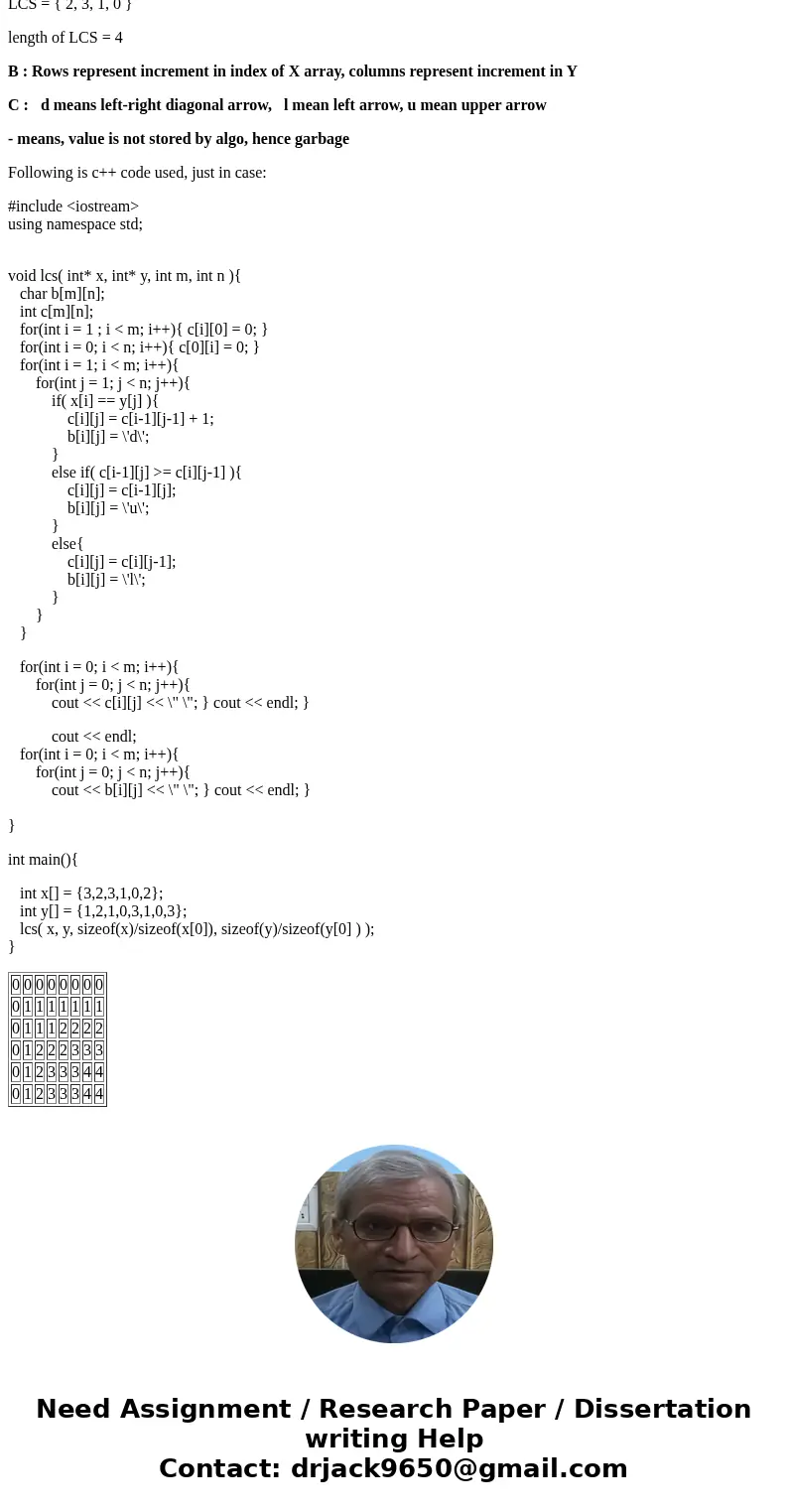
0	0	0	0	0	0	0	0
0	1	1	1	1	1	1	1
0	1	1	1	2	2	2	2
0	1	2	2	2	3	3	3
0	1	2	3	3	3	4	4
0	1	2	3	3	3	4	4