Question 3 Perform a regression analysis using compa as the

Question 3)

Perform a regression analysis using compa as the dependent variable and the same independent variables as used in question 2. (Question #2 found below the table). Show the result, and interpret your findings by answering the same questions.

Note: be sure to include the appropriate hypothesis statements.

A ) Regression hypotheses

Ho:

Ha:

Coefficient hyhpotheses (one to stand for all the separate variables)

Ho:

Ha:

B )Interpretation:

For the Regression as a whole:

What is the value of the F statistic:

What is the p-value associated with this value:

Is the p-value < 0.05?

Do you reject or not reject the null hypothesis:

What does this decision mean for our equal pay question (Do M and F get paid equaly?):

C )For each of the coefficients: Intercept, Midpoint, Age, Perf. rating, Service, Gender, Degree

What is the coefficient\'s p-value for each of the variables:

Is the p-value < 0.05?

Do you reject or not reject each null hypothesis:

What are the coefficients for the significant variables?

Using only the significant variables, what is the equation?  Compa =

Is gender a significant factor in compa:

If so, who gets paid more with all other things being equal?

How do we know?

ID

Salary

Compa

Midpoint

Age

Performance Rating

Service

Gender

Raise

Degree

Gender1

Gr

1

66.1

1.159

57

34

85

8

0

5.7

0

M

E

2

25.9

0.834

31

52

80

7

0

3.9

0

M

B

3

35.2

1.135

31

30

75

5

1

3.6

1

F

B

4

55.3

0.971

57

42

100

16

0

5.5

1

M

E

5

49.6

1.033

48

36

90

16

0

5.7

1

M

D

6

78.3

1.168

67

36

70

12

0

4.5

1

M

F

7

42.3

1.058

40

32

100

8

1

5.7

1

F

C

8

22.8

0.990

23

32

90

9

1

5.8

1

F

A

9

78

1.164

67

49

100

10

0

4

1

M

F

10

23.3

1.014

23

30

80

7

1

4.7

1

F

A

11

23.6

1.025

23

41

100

19

1

4.8

1

F

A

12

60.8

1.067

57

52

95

22

0

4.5

0

M

E

13

40.6

1.014

40

30

100

2

1

4.7

0

F

C

14

21.7

0.943

23

32

90

12

1

6

1

F

A

15

21.8

0.949

23

32

80

8

1

4.9

1

F

A

16

37.4

0.934

40

44

90

4

0

5.7

0

M

C

17

57

1.000

57

27

55

3

1

3

1

F

E

18

33.5

1.081

31

31

80

11

1

5.6

0

F

B

19

23

1.000

23

32

85

1

0

4.6

1

M

A

20

36

1.162

31

44

70

16

1

4.8

0

F

B

21

76

1.135

67

43

95

13

0

6.3

1

M

F

22

43.7

0.911

48

48

65

6

1

3.8

1

F

D

23

25.3

1.098

23

36

65

6

1

3.3

0

F

A

24

48.9

1.019

48

30

75

9

1

3.8

0

F

D

25

25.8

1.122

23

41

70

4

0

4

0

M

A

26

23.3

1.013

23

22

95

2

1

6.2

0

F

A

27

42.3

1.057

40

35

80

7

0

3.9

1

M

C

28

75.2

1.122

67

44

95

9

1

4.4

0

F

F

29

80.9

1.208

67

52

95

5

0

5.4

0

M

F

30

49

1.020

48

45

90

18

0

4.3

0

M

D

31

24.2

1.054

23

29

60

4

1

3.9

1

F

A

32

27.5

0.886

31

25

95

4

0

5.6

0

M

B

33

63.6

1.115

57

35

90

9

0

5.5

1

M

E

34

28.6

0.922

31

26

80

2

0

4.9

1

M

B

35

22.4

0.976

23

23

90

4

1

5.3

0

F

A

36

23.6

1.026

23

27

75

3

1

4.3

0

F

A

37

24.3

1.057

23

22

95

2

1

6.2

0

F

A

38

63

1.105

57

45

95

11

0

4.5

0

M

E

39

34.8

1.123

31

27

90

6

1

5.5

0

F

B

40

24.3

1.057

23

24

90

2

0

6.3

0

M

A

41

42.8

1.071

40

25

80

5

0

4.3

0

M

C

42

23

0.998

23

32

100

8

1

5.7

1

F

A

43

75.4

1.125

67

42

95

20

1

5.5

0

F

F

44

60.7

1.065

57

45

90

16

0

5.2

1

M

E

45

57.9

1.206

48

36

95

8

1

5.2

1

F

D

46

62.2

1.091

57

39

75

20

0

3.9

1

M

E

47

62.2

1.091

57

37

95

5

0

5.5

1

M

E

48

70.1

1.230

57

34

90

11

1

5.3

1

F

E

49

61.7

1.083

57

41

95

21

0

6.6

0

M

E

50

61.4

1.077

57

38

80

12

0

4.6

0

M

E

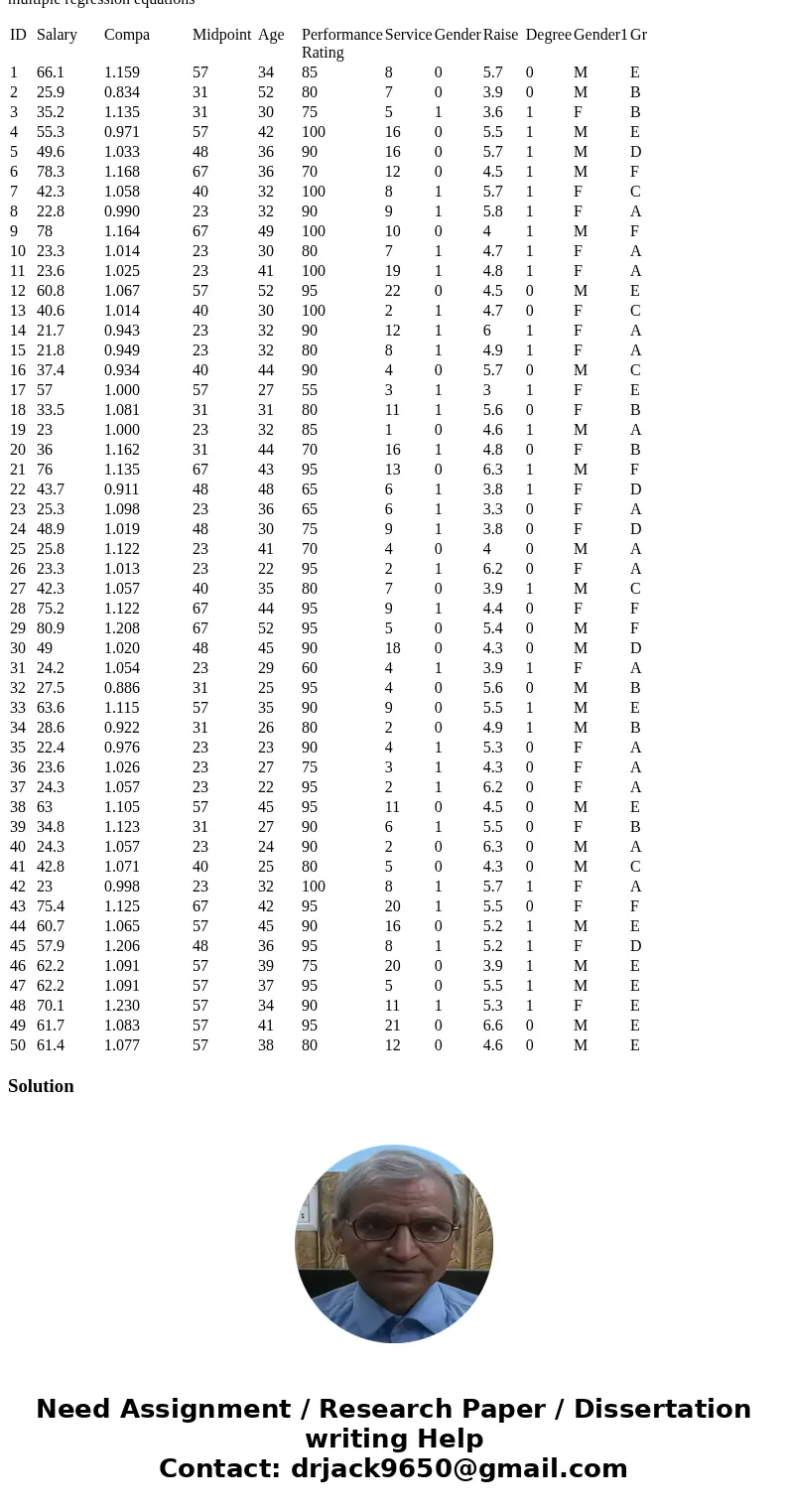
Question 2)

Below is a regression analysis for salary being predicted/explained by the other variables in our sample (Midpoint,  age, performance rating, service, gender, and degree variables. (Note: since salary and compa are different ways of  expressing an employee’s salary, we do not want to have both used in the same regression.)

Plase interpret the findings. ( Note: technically we have one for each input variable.  Listing it this way to save space.)

Ho: The regression equation is not significant.

Ha: The regression equation is significant.

Ho: The regression coefficient for each variable is not significant

Ha: The regression coefficient for each variable is significant

Sal

SUMMARY OUTPUT

Regression Statistics

Multiple R

0.991559074655531

R Square

0.983189398531733

Adjusted R Square

0.98084373321058

Standard Error

2.65759257261024

Observations

50

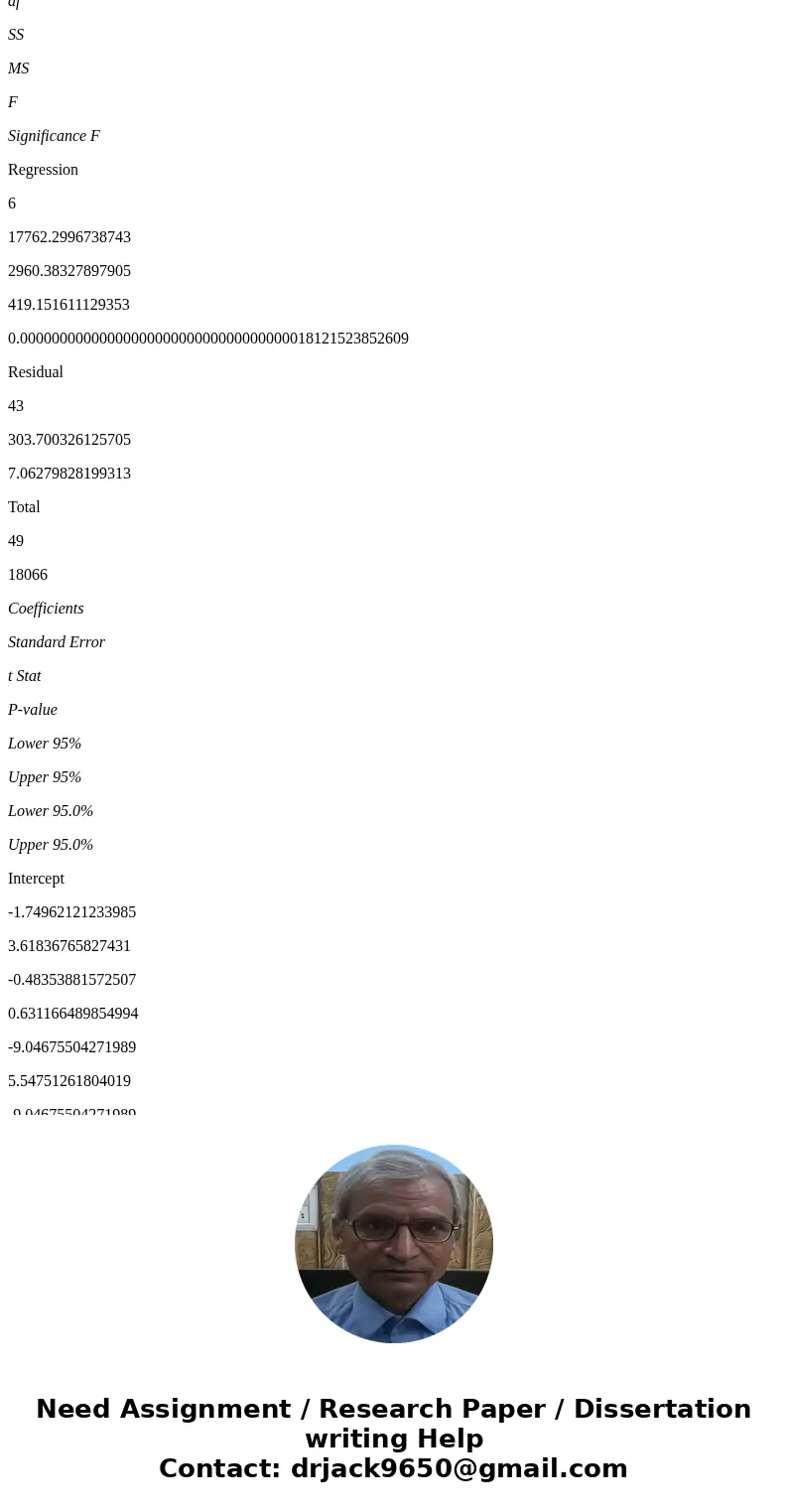
ANOVA

df

SS

MS

F

Significance F

Regression

6

17762.2996738743

2960.38327897905

419.151611129353

0.0000000000000000000000000000000000018121523852609

Residual

43

303.700326125705

7.06279828199313

Total

49

18066

Coefficients

Standard Error

t Stat

P-value

Lower 95%

Upper 95%

Lower 95.0%

Upper 95.0%

Intercept

-1.74962121233985

3.61836765827431

-0.48353881572507

0.631166489854994

-9.04675504271989

5.54751261804019

-9.04675504271989

5.54751261804019

Midpoint

1.21670105053015

0.0319023509083532

38.1382881163022

0.0000000000000000000000000000000000866416336978111

1.15236382831625

1.28103827274406

1.15236382831625

1.28103827274406

Age

-0.00462801024512803

0.0651972120227729

-0.0709847875628716

0.943738987458078

-0.136110719142857

0.126854698652601

-0.136110719142857

0.126854698652601

Performace Rating

-0.0565964405497542

0.0344950678086454

-1.64071109712588

0.108153181882588

-0.126162374711284

0.0129694936117759

-0.126162374711284

0.0129694936117759

Service

-0.0425003573420269

0.0843369820842078

-0.503935003265728

0.616879351918047

-0.212582091217666

0.127581376533612

-0.212582091217666

0.127581376533612

Gender

2.42033721201279

0.860844317571592

2.81158528041454

0.00739661875026853

0.684279192016561

4.15639523200902

0.684279192016561

4.15639523200902

Degree

0.275533414317469

0.799802304805058

0.344501900859896

0.732148118953479

-1.33742165470733

1.88848848334226

-1.33742165470733

1.88848848334226

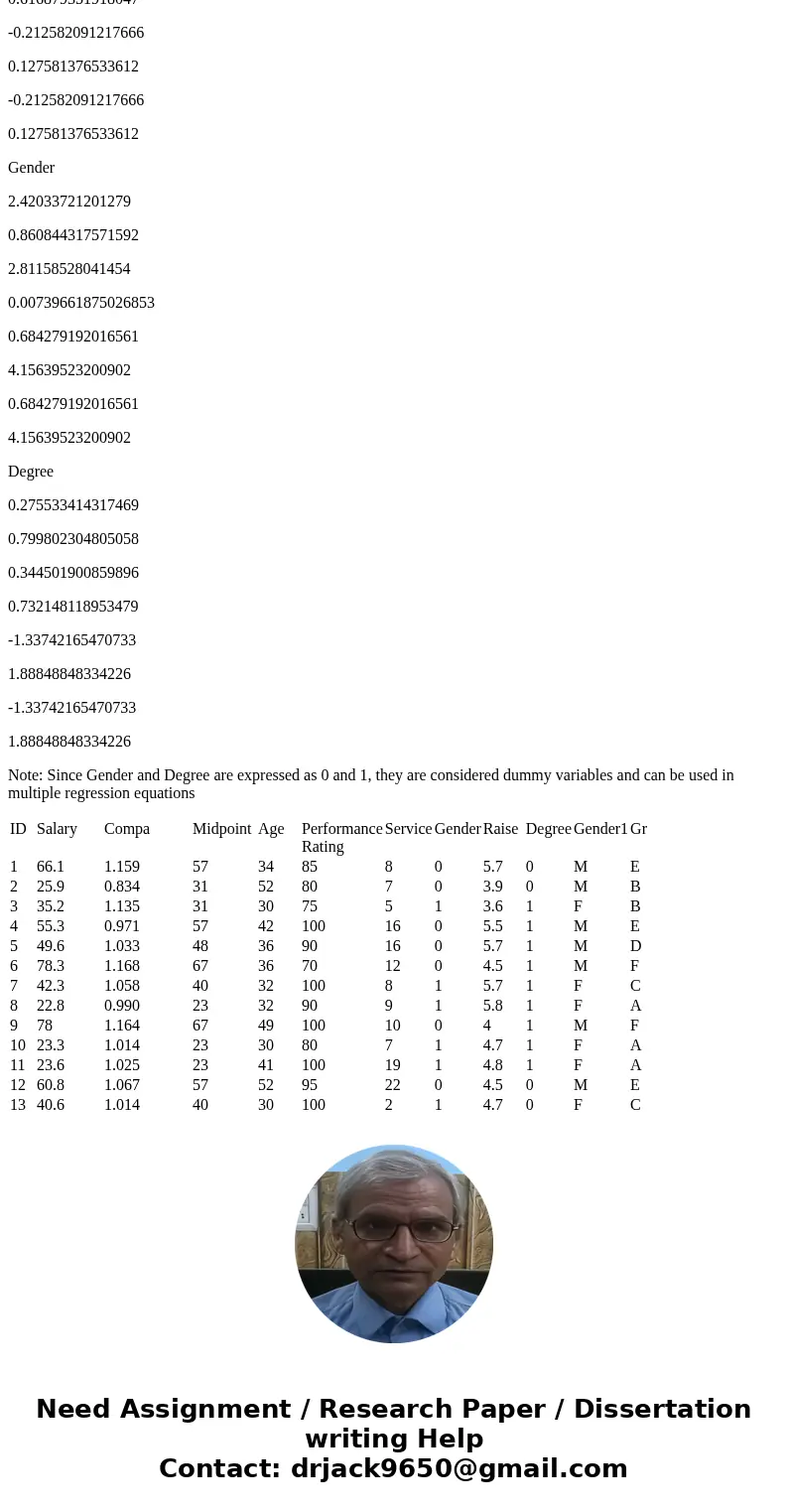
Note: Since Gender and Degree are expressed as 0 and 1, they are considered dummy variables and can be used in multiple regression equations

ID	Salary	Compa	Midpoint	Age	Performance Rating	Service	Gender	Raise	Degree	Gender1	Gr
1	66.1	1.159	57	34	85	8	0	5.7	0	M	E
2	25.9	0.834	31	52	80	7	0	3.9	0	M	B
3	35.2	1.135	31	30	75	5	1	3.6	1	F	B
4	55.3	0.971	57	42	100	16	0	5.5	1	M	E
5	49.6	1.033	48	36	90	16	0	5.7	1	M	D
6	78.3	1.168	67	36	70	12	0	4.5	1	M	F
7	42.3	1.058	40	32	100	8	1	5.7	1	F	C
8	22.8	0.990	23	32	90	9	1	5.8	1	F	A
9	78	1.164	67	49	100	10	0	4	1	M	F
10	23.3	1.014	23	30	80	7	1	4.7	1	F	A
11	23.6	1.025	23	41	100	19	1	4.8	1	F	A
12	60.8	1.067	57	52	95	22	0	4.5	0	M	E
13	40.6	1.014	40	30	100	2	1	4.7	0	F	C
14	21.7	0.943	23	32	90	12	1	6	1	F	A
15	21.8	0.949	23	32	80	8	1	4.9	1	F	A
16	37.4	0.934	40	44	90	4	0	5.7	0	M	C
17	57	1.000	57	27	55	3	1	3	1	F	E
18	33.5	1.081	31	31	80	11	1	5.6	0	F	B
19	23	1.000	23	32	85	1	0	4.6	1	M	A
20	36	1.162	31	44	70	16	1	4.8	0	F	B
21	76	1.135	67	43	95	13	0	6.3	1	M	F
22	43.7	0.911	48	48	65	6	1	3.8	1	F	D
23	25.3	1.098	23	36	65	6	1	3.3	0	F	A
24	48.9	1.019	48	30	75	9	1	3.8	0	F	D
25	25.8	1.122	23	41	70	4	0	4	0	M	A
26	23.3	1.013	23	22	95	2	1	6.2	0	F	A
27	42.3	1.057	40	35	80	7	0	3.9	1	M	C
28	75.2	1.122	67	44	95	9	1	4.4	0	F	F
29	80.9	1.208	67	52	95	5	0	5.4	0	M	F
30	49	1.020	48	45	90	18	0	4.3	0	M	D
31	24.2	1.054	23	29	60	4	1	3.9	1	F	A
32	27.5	0.886	31	25	95	4	0	5.6	0	M	B
33	63.6	1.115	57	35	90	9	0	5.5	1	M	E
34	28.6	0.922	31	26	80	2	0	4.9	1	M	B
35	22.4	0.976	23	23	90	4	1	5.3	0	F	A
36	23.6	1.026	23	27	75	3	1	4.3	0	F	A
37	24.3	1.057	23	22	95	2	1	6.2	0	F	A
38	63	1.105	57	45	95	11	0	4.5	0	M	E
39	34.8	1.123	31	27	90	6	1	5.5	0	F	B
40	24.3	1.057	23	24	90	2	0	6.3	0	M	A
41	42.8	1.071	40	25	80	5	0	4.3	0	M	C
42	23	0.998	23	32	100	8	1	5.7	1	F	A
43	75.4	1.125	67	42	95	20	1	5.5	0	F	F
44	60.7	1.065	57	45	90	16	0	5.2	1	M	E
45	57.9	1.206	48	36	95	8	1	5.2	1	F	D
46	62.2	1.091	57	39	75	20	0	3.9	1	M	E
47	62.2	1.091	57	37	95	5	0	5.5	1	M	E
48	70.1	1.230	57	34	90	11	1	5.3	1	F	E
49	61.7	1.083	57	41	95	21	0	6.6	0	M	E
50	61.4	1.077	57	38	80	12	0	4.6	0	M	E

Solution