The following linear programming problem has been solved by

The following linear programming problem has been solved by EXCEL. Use the output to answer the following questions.

                      

Max

4X₁ + 5X₂ + 6X₃

s.t.

X₁ + X₂ + X₃ 85

(Production capacity)

X₁ + 4X₂ + X₃ 280

(Material A requirements)

X₁ + 4X₂ + 4X₃ 320

(Material B requirements)

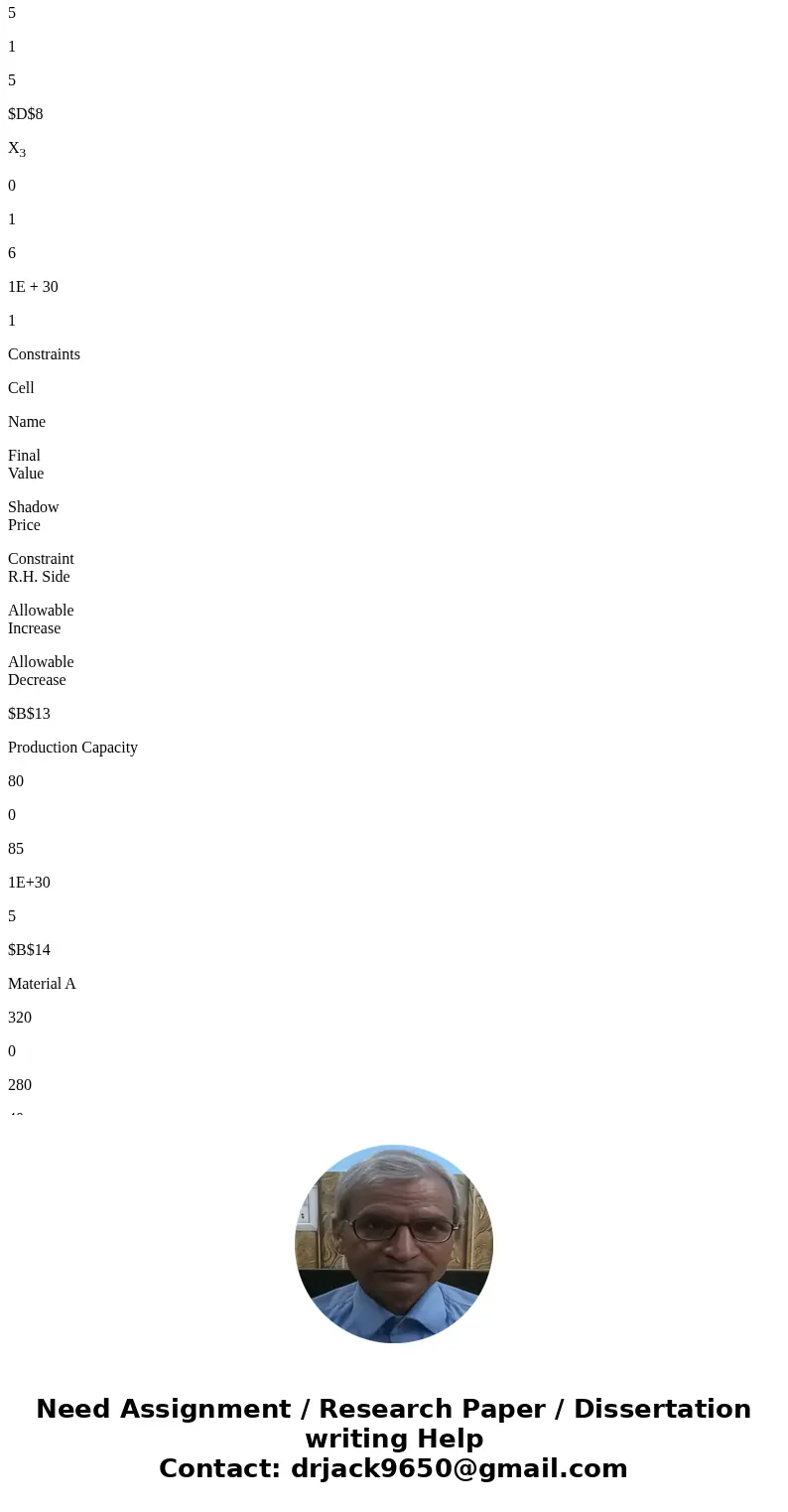
Cell

Name

Final
Value

Reduced
Cost

Objective
Coefficient

Allowable
Increase

Allowable
Decrease

$B$8

X₁

0

1.5

4

1E + 30

1.5

$C$8

X₂

80

0

5

1

5

$D$8

X₃

0

1

6

1E + 30

1

Constraints

Cell

Name

Final
Value

Shadow
Price

Constraint
R.H. Side

Allowable
Increase

Allowable
Decrease

$B$13

Production Capacity

80

0

85

1E+30

5

$B$14

Material A

320

0

280

40

1E+30

$B$15

Material B

320

1.25

320

20

40

1.  What are the shadow prices for each resource? Interpret.

2. What are the reduced costs? Interpret them in this context.

3.  Compute and interpret the ranges of optimality.

4. Compute and interpret the ranges of feasibility.

Max	4X1 + 5X2 + 6X3
s.t.	X1 + X2 + X3 85	(Production capacity)
	X1 + 4X2 + X3 280	(Material A requirements)
	X1 + 4X2 + 4X3 320	(Material B requirements)

Solution

The problem is that of product mix, there are three types of products represented by variables X1, X2 and X3 and three constraints in terms of Production capacity, MaterialA and MaterialB

The given solution is not optimal, the optimal solution is X1=0, X2=65 and X3=20 with value of the objective function 445 as against the given solution with value of objective function as 400.

In the given tables of question Shadow prices of Production capacity and MaterialA are shown as zeros and shadow price of MaterialB as 1.25

Reduced costs as per the given tables are 1.5 for X1, zero for X2 and 1 for X3

The given solution is feasible but as stated above is not optimal and can be improved by introducing X3 into the basis. Under the given solution Production capacity is underutilized

Computation of the Ranging under the optimal solution is given in the following table;

Variable	Value	Reduced cost	Original value	Lower Bound	Upper Bound
X1	0	2	4	-infinity	6
X3	65	0	5	-infinity	6
X3	20	0	6	5	infinity
Constraint	Dual Value	Slack/surplus	original Value	Lower bound	Upper bound
Production	6.333	0	85	80	280
MaterialA	-.3333	0	280	85	340
MaterialB	0	20	320	-infinity	340