You are working for a government department and your boss Ja

You are working for a government department and your boss, Jane, has asked you to calculate some results on weekly household income across the state, including a 95% confidence interval for the mean weekly household income that she needs to include in a report. She also says that she is not sure exactly what a 95% confidence interval means and would like you to add an explanation.

You have been supplied with a sample of weekly income figures for 110 households. The data is presented here:

Download the data

Historically, the standard deviation in weekly household income is $480.

Complete the report to your boss. Give your numeric answers to 2 decimal places.

Dear Jane,

Here are the results gathered from the collected data:

Assuming a population standard deviation in weekly household income of $480, the 95% confidence interval for the mean weekly household income is:

a) ? ? ?

b)This means that

approximately 95% of sample means will be within the interval given above
on approximately 95% of days in a given period the stock makes a return within the interval given above
the population mean weekly household income is definitely within the interval given above
using a process that gives correct results in 95% of cases, the population mean weekly household income is within the interval given above

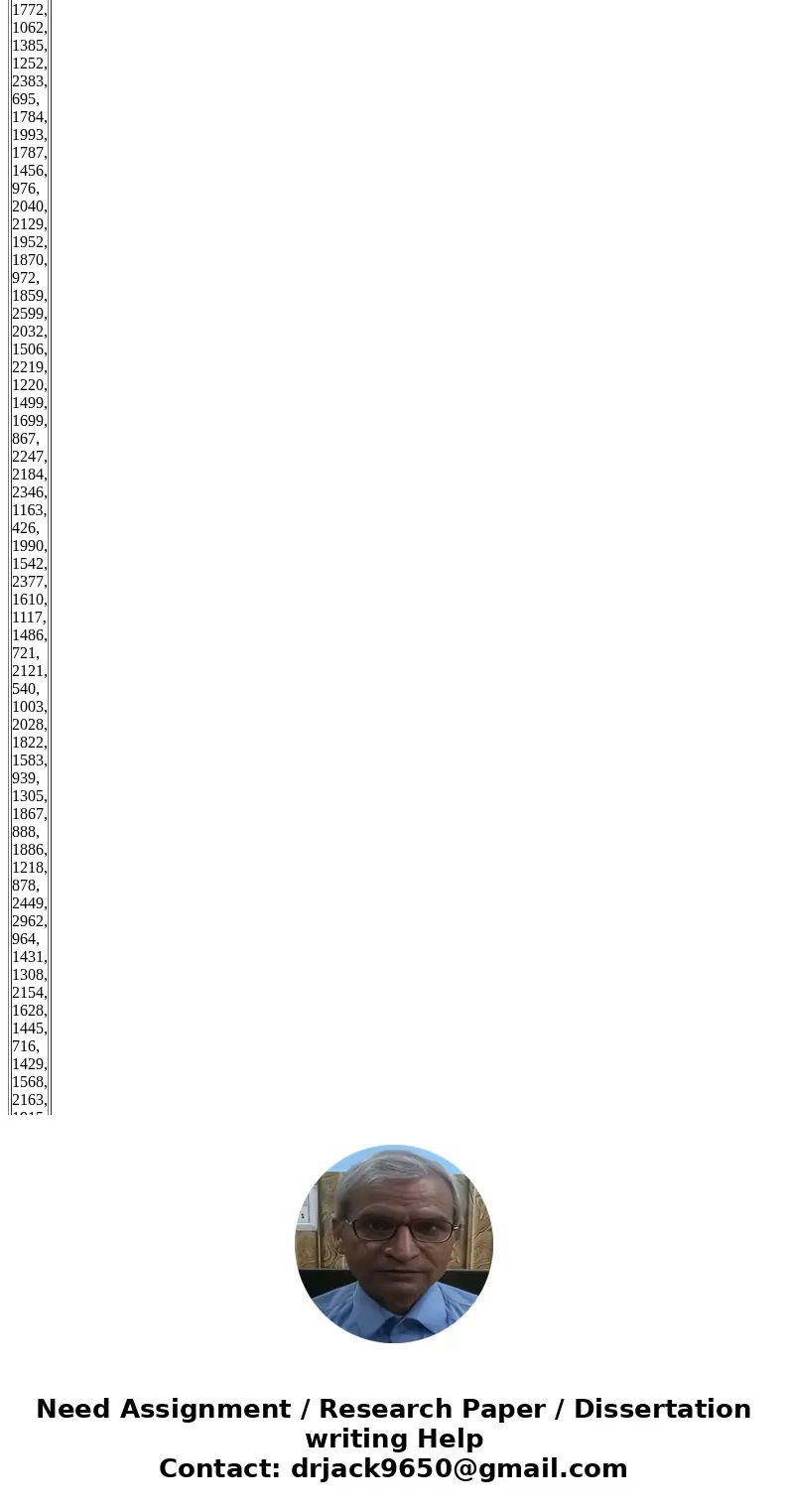
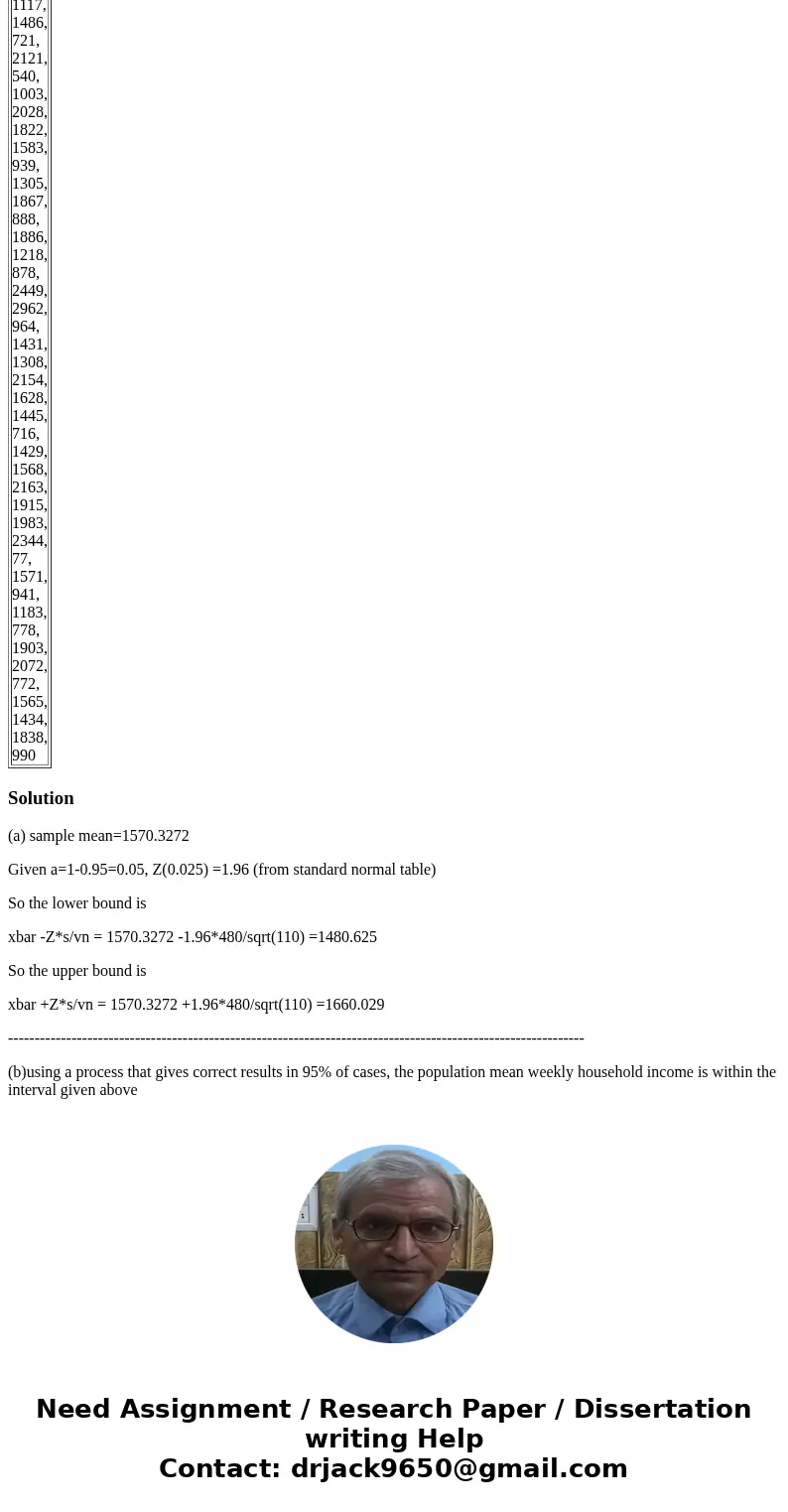
2807,
358,
1407,
1488,
1090,
2047,
2029,
1681,
1061,
668,
2091,
1241,
2398,
1516,
1662,
1853,
1332,
1643,
834,
1434,
2243,
2172,
2254,
2147,
2212,
1316,
2107,
1426,
408,
1565,
2017,
961,
1390,
1772,
1062,
1385,
1252,
2383,
695,
1784,
1993,
1787,
1456,
976,
2040,
2129,
1952,
1870,
972,
1859,
2599,
2032,
1506,
2219,
1220,
1499,
1699,
867,
2247,
2184,
2346,
1163,
426,
1990,
1542,
2377,
1610,
1117,
1486,
721,
2121,
540,
1003,
2028,
1822,
1583,
939,
1305,
1867,
888,
1886,
1218,
878,
2449,
2962,
964,
1431,
1308,
2154,
1628,
1445,
716,
1429,
1568,
2163,
1915,
1983,
2344,
77,
1571,
941,
1183,
778,
1903,
2072,
772,
1565,
1434,
1838,
990

(a) sample mean=1570.3272

Given a=1-0.95=0.05, Z(0.025) =1.96 (from standard normal table)

So the lower bound is

xbar -Z*s/vn = 1570.3272 -1.96*480/sqrt(110) =1480.625

So the upper bound is

xbar +Z*s/vn = 1570.3272 +1.96*480/sqrt(110) =1660.029

-------------------------------------------------------------------------------------------------------------

(b)using a process that gives correct results in 95% of cases, the population mean weekly household income is within the interval given above