A rat has to choose between 5 doors one of which contains ch

A rat has to choose between 5 doors, one of which contains chocolate. If the rat chooses the wrong door, it is returned to the starting point and chooses again, and continues until it gets the chocolate. Let X be the serial number of the trial on which the chocolate is found. (a) Find the probability function of X. (b) What is the expectation of X?

Solution

Probabibility function:

Here, point is, if rat goes to wrong door, and again rat goes for chocolate, it dont know that which door it visited earlier.

So,

P(x>=n) = 1/5 + 4/5 * 1/5 + 4/5*4/5 * 1/5 + .......+ (4/5)^(n-1) * 1/5

So, P(x>=n) = 1/5 ( 1+ 4/5 + (4/5)^2+.....+(4/5)^(n-1))

So, P(x>=n) = 1/5 * 1 * (1-(4/5)^(n-1)) / (1-4/5)

So, P(x>=n) = 1 - (4/5)^(n-1)

P(n=r) = P(n>=r) - P(n>= (r-1)) = (4/5)^(r-1) - (4/5)^(r-2)

Now,

expected value,

E(x) = Sum of (P(x=i) * i)

where i = nos of trial.

By doing in excel,

So, Expected value = 4.9999 (almost near to 5)

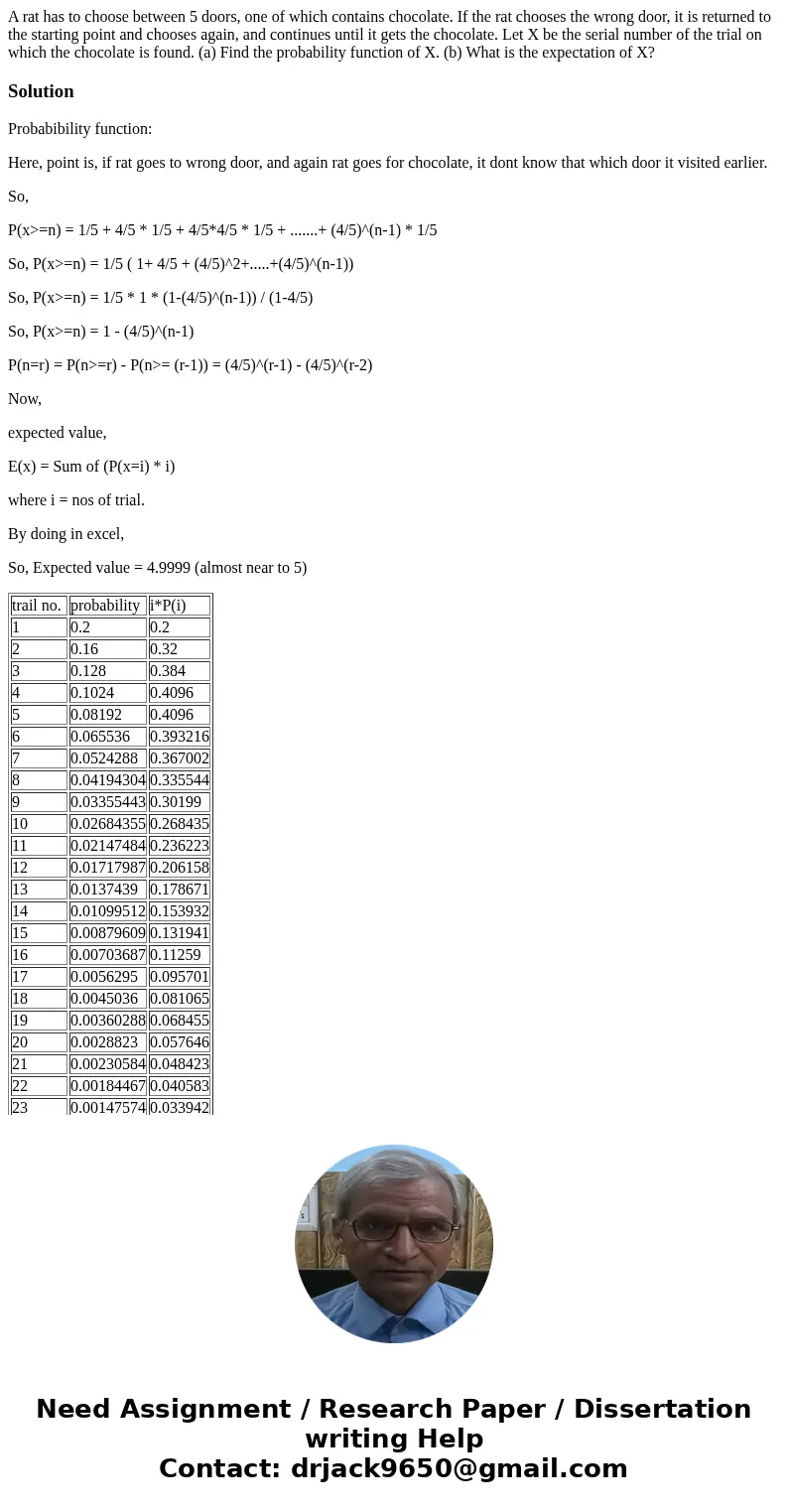
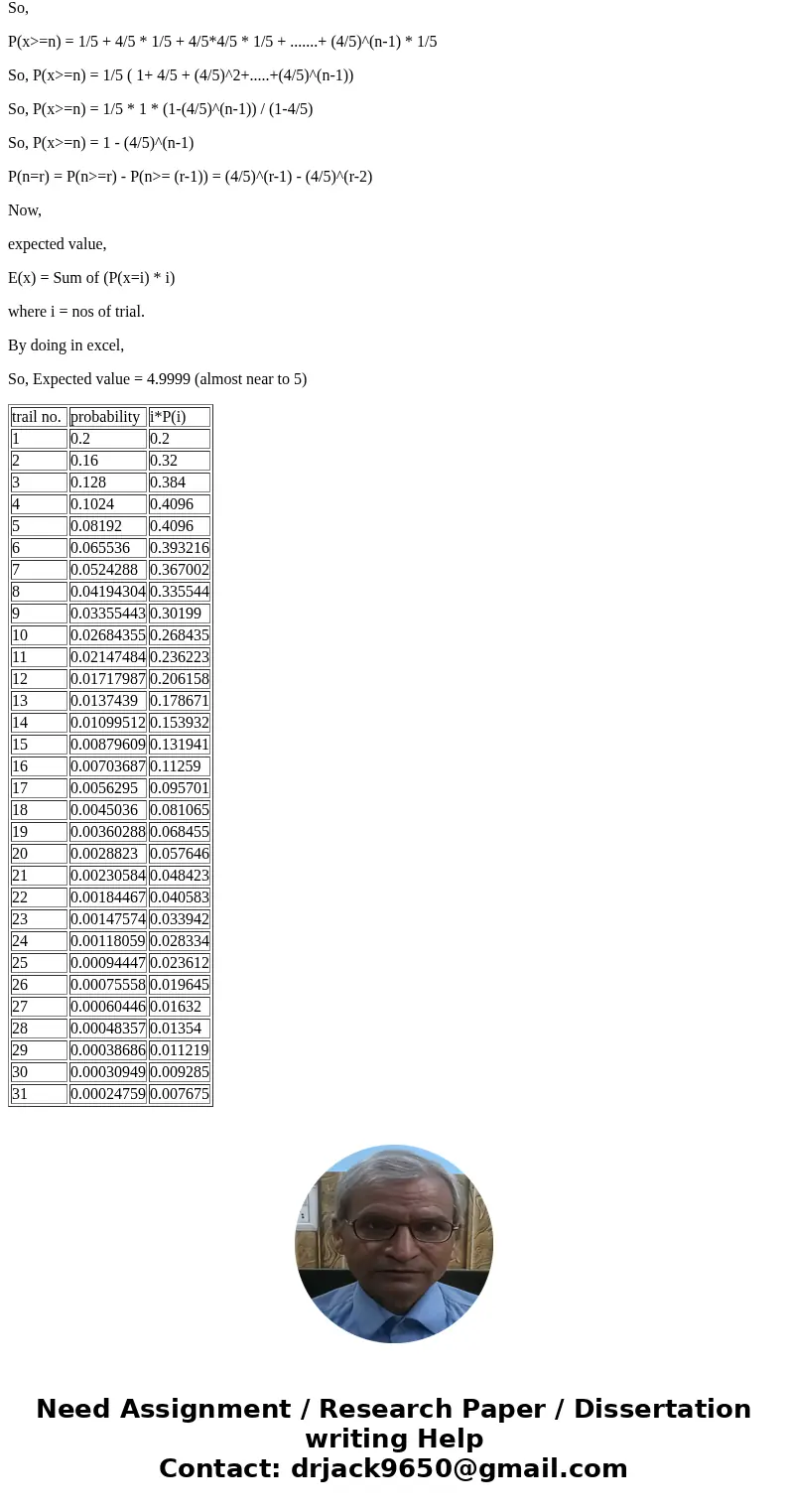
trail no.	probability	i*P(i)
1	0.2	0.2
2	0.16	0.32
3	0.128	0.384
4	0.1024	0.4096
5	0.08192	0.4096
6	0.065536	0.393216
7	0.0524288	0.367002
8	0.04194304	0.335544
9	0.03355443	0.30199
10	0.02684355	0.268435
11	0.02147484	0.236223
12	0.01717987	0.206158
13	0.0137439	0.178671
14	0.01099512	0.153932
15	0.00879609	0.131941
16	0.00703687	0.11259
17	0.0056295	0.095701
18	0.0045036	0.081065
19	0.00360288	0.068455
20	0.0028823	0.057646
21	0.00230584	0.048423
22	0.00184467	0.040583
23	0.00147574	0.033942
24	0.00118059	0.028334
25	0.00094447	0.023612
26	0.00075558	0.019645
27	0.00060446	0.01632
28	0.00048357	0.01354
29	0.00038686	0.011219
30	0.00030949	0.009285
31	0.00024759	0.007675