Condense 3 log x 4 log y log x3y4 log yx12 log yx logxy12

Condense 3 log x - 4 log y log = x^3/y^4 log (yx)^12 -log yx log(x/y)^12 Condense log_9 x/2 + log_9 y/2 + log_9 z/2 2 log 9 (xyz)^2 2log_9 xyz log_9 xyz/2 log_9 squareroot xyz Expand log_8 (u^6 middot v)^3 6 log_8 v + log_8 u/3 log_8 u/3) + log_8 v/3 18 log_8 u + 3 log_8 v 9 log_8 u + 4 log_8 v Expand log_9 (z^5 cube squareroot x) 3 log_9 x + 5 log_9 z 5 log_9 z + log_9 x/3 5 log_9 z - 5 log_9 x log_9 z + log_9 x/3 Identify the domain and range of the given: y = log_2 (x + 4) + 4 Domain: All reals Range: x -4 Range: All reals Domain: All reals Range: x > 4 Domain: x > 4 Range: All reals Using the given: y = -1/2 middot log_4 x + 3 of the following is not ture? a reflection over y axis a vertical shift up 3 an asymptote at x = 0 a shrink by 1/2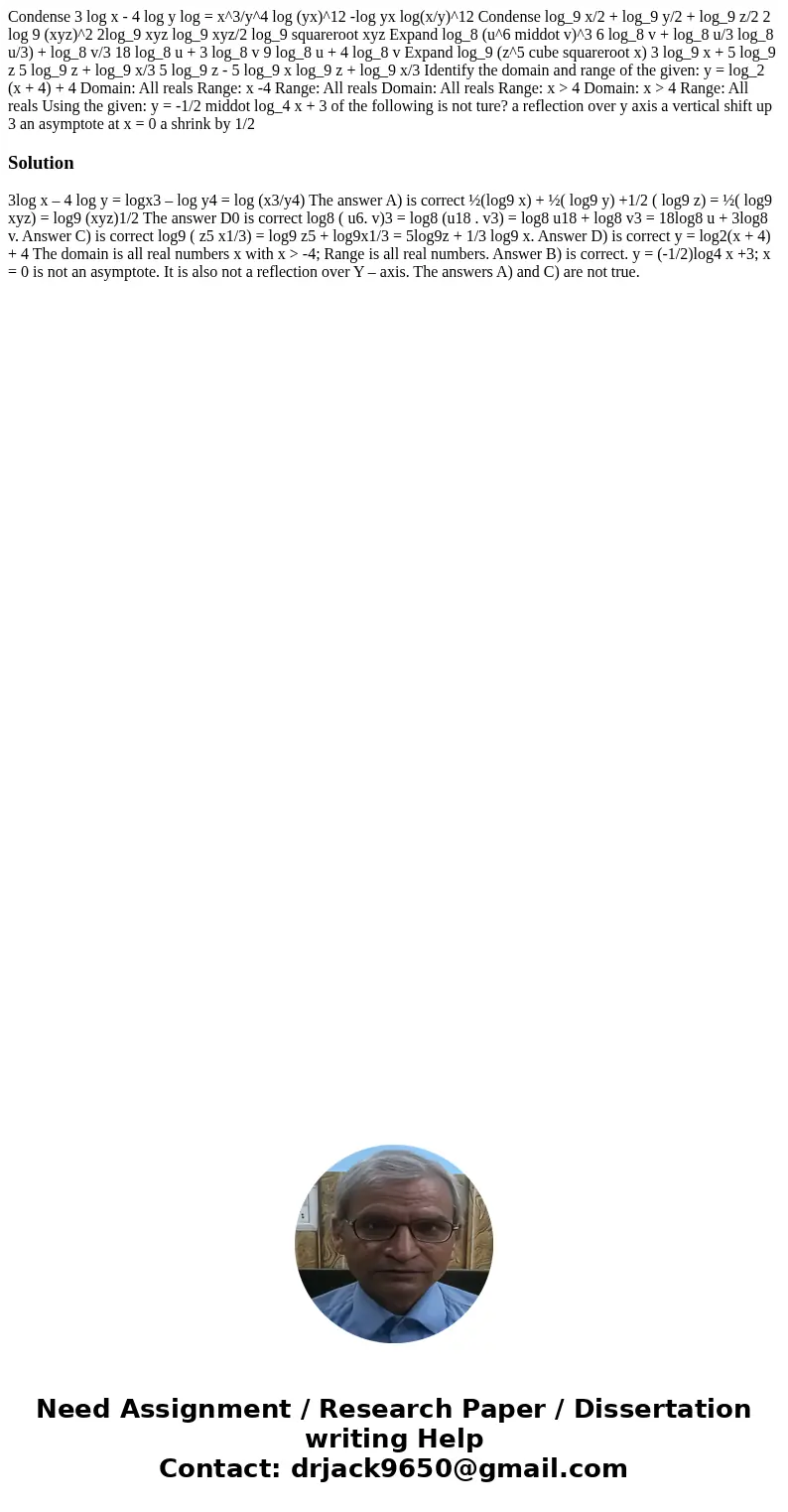

Solution

3log x – 4 log y = logx3 – log y4 = log (x3/y4) The answer A) is correct ½(log9 x) + ½( log9 y) +1/2 ( log9 z) = ½( log9 xyz) = log9 (xyz)1/2 The answer D0 is correct log8 ( u6. v)3 = log8 (u18 . v3) = log8 u18 + log8 v3 = 18log8 u + 3log8 v. Answer C) is correct log9 ( z5 x1/3) = log9 z5 + log9x1/3 = 5log9z + 1/3 log9 x. Answer D) is correct y = log2(x + 4) + 4 The domain is all real numbers x with x > -4; Range is all real numbers. Answer B) is correct. y = (-1/2)log4 x +3; x = 0 is not an asymptote. It is also not a reflection over Y – axis. The answers A) and C) are not true.