Based on sample results assume that human body temperatures

Based on sample results, assume that human body temperatures are normally distributed with a mean of 98.20F and a standard dev. of 0.62F

1. what is the percentage of normal and healthy people whose body temperatures are above 97.88F
2. what is the percentage of normal and healthy people whose body temperatures are between 97.88F and 100F
3. XXX hospital in Dududutto uses 100F as the lowest temp considered to be a fever. What percnetage of normal and healthy people would be coonsidered to have a ffever?
4. Physicians want to select a min temperature for requring further medical tests. What should that temperature be, if we want only 5% of healthy people to exceed it?

(Answer with explanation please)

Solution

1.

We first get the z score for the critical value. As z = (x - u) / s, then as          
          
x = critical value =    97.88      
u = mean =    98.2      
          
s = standard deviation =    0.62      
          
Thus,          
          
z = (x - u) / s =    -0.516129032      
          
Thus, using a table/technology, the right tailed area of this is          
          
P(z >   -0.516129032   ) =    0.697117854 [ANSWER]

*****************

2.

We first get the z score for the two values. As z = (x - u) / s, then as          
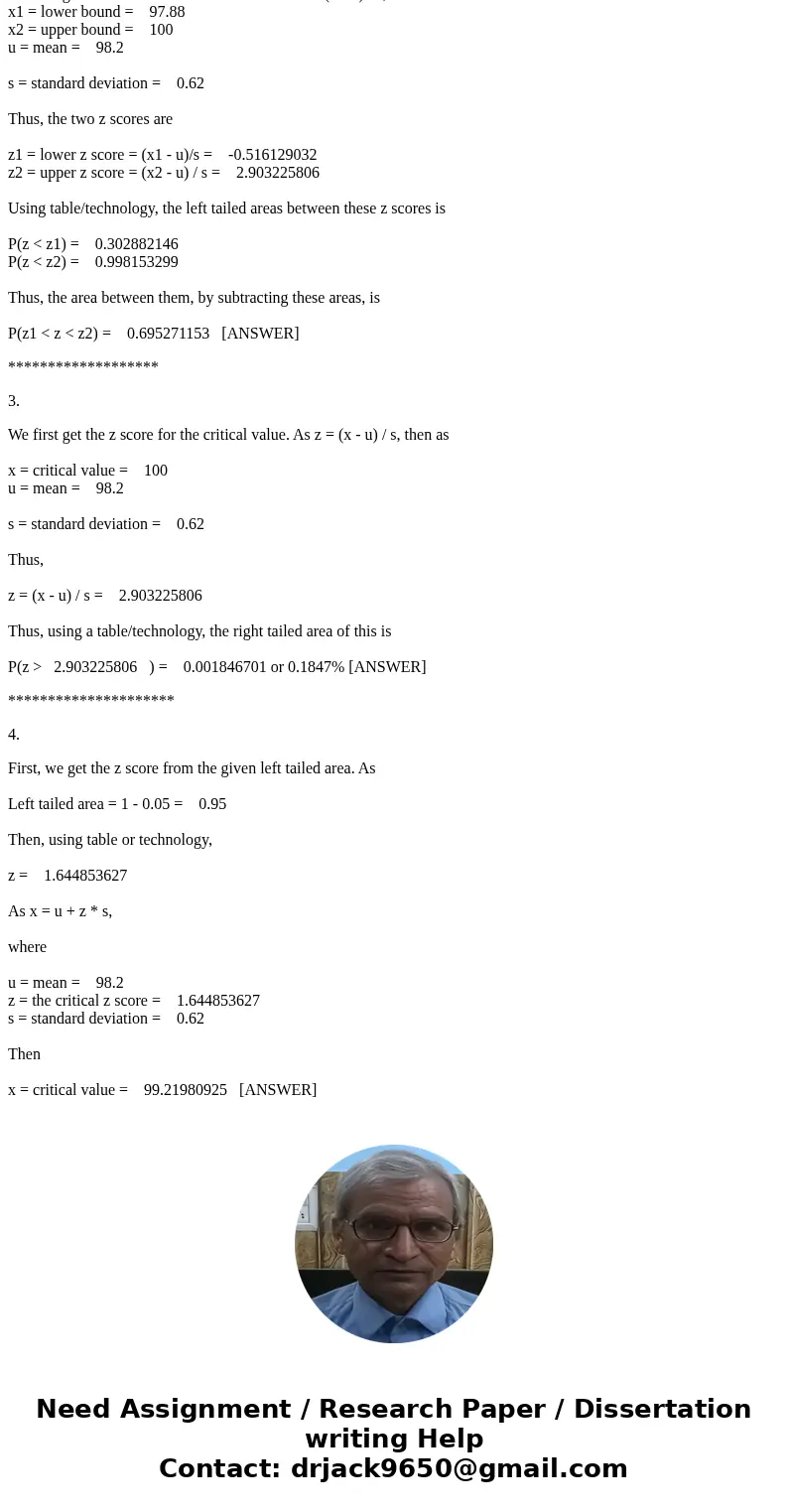
x1 = lower bound =    97.88      
x2 = upper bound =    100      
u = mean =    98.2      
          
s = standard deviation =    0.62      
          
Thus, the two z scores are          
          
z1 = lower z score = (x1 - u)/s =    -0.516129032      
z2 = upper z score = (x2 - u) / s =    2.903225806      
          
Using table/technology, the left tailed areas between these z scores is          
          
P(z < z1) =    0.302882146      
P(z < z2) =    0.998153299      
          
Thus, the area between them, by subtracting these areas, is          
          
P(z1 < z < z2) =    0.695271153   [ANSWER]

*******************

3.

We first get the z score for the critical value. As z = (x - u) / s, then as          
          
x = critical value =    100      
u = mean =    98.2      
          
s = standard deviation =    0.62      
          
Thus,          
          
z = (x - u) / s =    2.903225806      
          
Thus, using a table/technology, the right tailed area of this is          
          
P(z >   2.903225806   ) =    0.001846701 or 0.1847% [ANSWER]

*********************

4.

First, we get the z score from the given left tailed area. As          
          
Left tailed area = 1 - 0.05 =    0.95      
          
Then, using table or technology,          
          
z =    1.644853627      
          
As x = u + z * s,          
          
where          
          
u = mean =    98.2      
z = the critical z score =    1.644853627      
s = standard deviation =    0.62      
          
Then          
          
x = critical value =    99.21980925   [ANSWER]