Homework SourseUse truth tables to determine which of the following formula
Use truth tables to determine which of the following formulas are equivalent to each other. Use truth tables to determine which of the following formulas are tautologies, which are contradictions, and which are neither. Use the laws stated in the text to find simpler formulas equivalent to these formulas. Explain the reasoning that you used to find your solution.
Solution
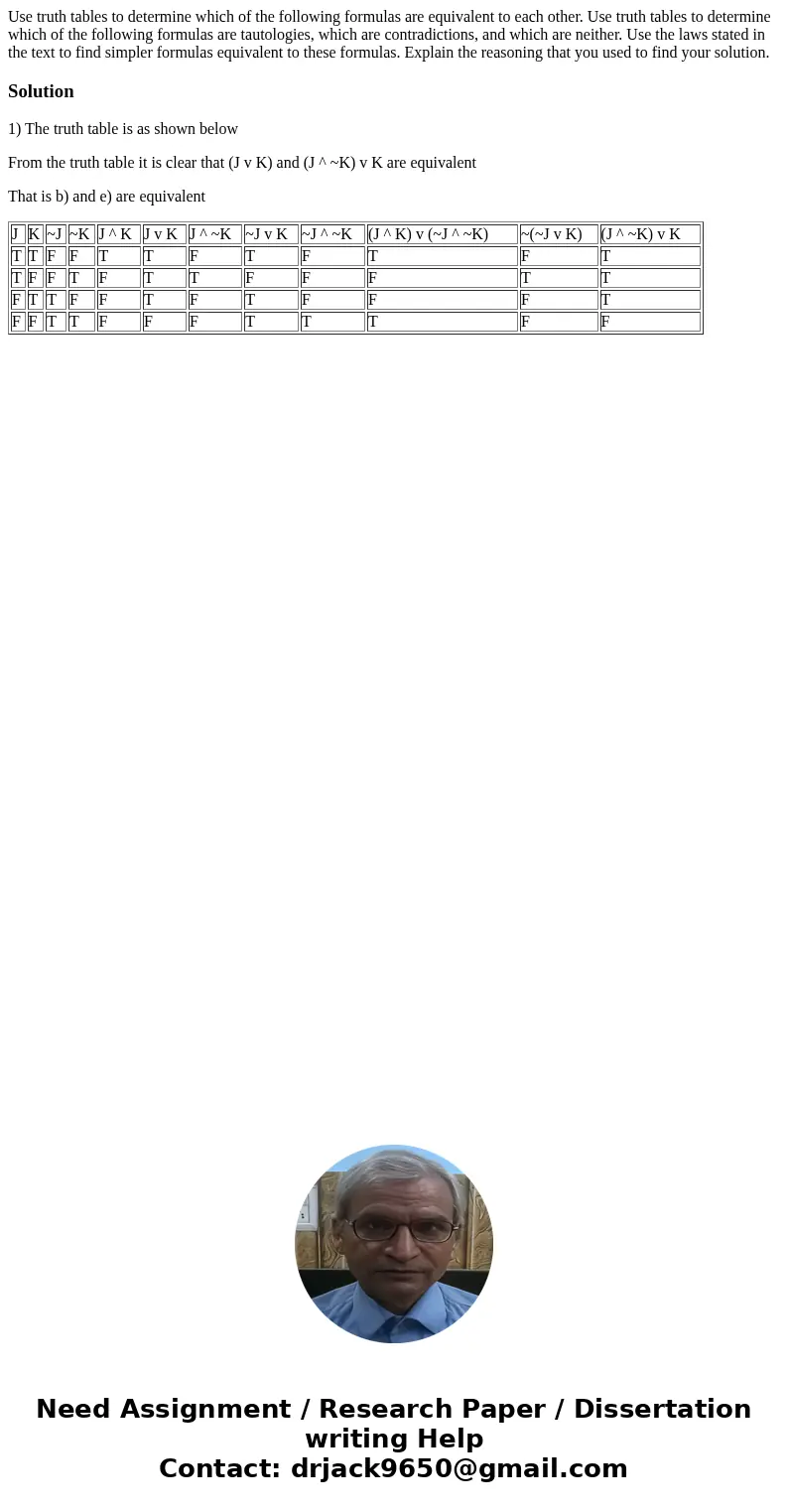
1) The truth table is as shown below
From the truth table it is clear that (J v K) and (J ^ ~K) v K are equivalent
That is b) and e) are equivalent
| J | K | ~J | ~K | J ^ K | J v K | J ^ ~K | ~J v K | ~J ^ ~K | (J ^ K) v (~J ^ ~K) | ~(~J v K) | (J ^ ~K) v K |
| T | T | F | F | T | T | F | T | F | T | F | T |
| T | F | F | T | F | T | T | F | F | F | T | T |
| F | T | T | F | F | T | F | T | F | F | F | T |
| F | F | T | T | F | F | F | T | T | T | F | F |
