The paired data below consists of test scores and hours of p
The paired data below consists of test scores and hours of preparation for 5 randomly selected students. Use this data set to answer the questions below: x Hours of preparation 5 2 9 6 10 y Test score 64 48 72 73 80 Find the standard error . Use formula or MS Excel.
Solution
Regression:
PART 1: Line of Regression Y on X i.e Y = bo + b1 X
Mean of X = X / n = 6.4
Mean of Y = Y / n = 67.4
(Xi - Mean)^2 = 41.2
(Yi - Mean)^2 = 599.2
(Xi-Mean)*(Yi-Mean) = 145.2
b1 = (Xi-Mean)*(Yi-Mean) / (Xi - Mean)^2
b1 = 145.2 / 41.2 = 3.5243
bo = Y / n - b1 * X / n
bo = 67.4 - 3.5243*6.4 = 44.8447
Y = bo + b1 X
Y\'=44.8447+3.5243*X
PART 2: Standard Error of Y on X i.e Y = bo + b1 X
Standard error = Sqrt( ( Y -Yi )^2/ n-2 )
Y -Yi )^2 = 87.463
Standard Error = 5.3995
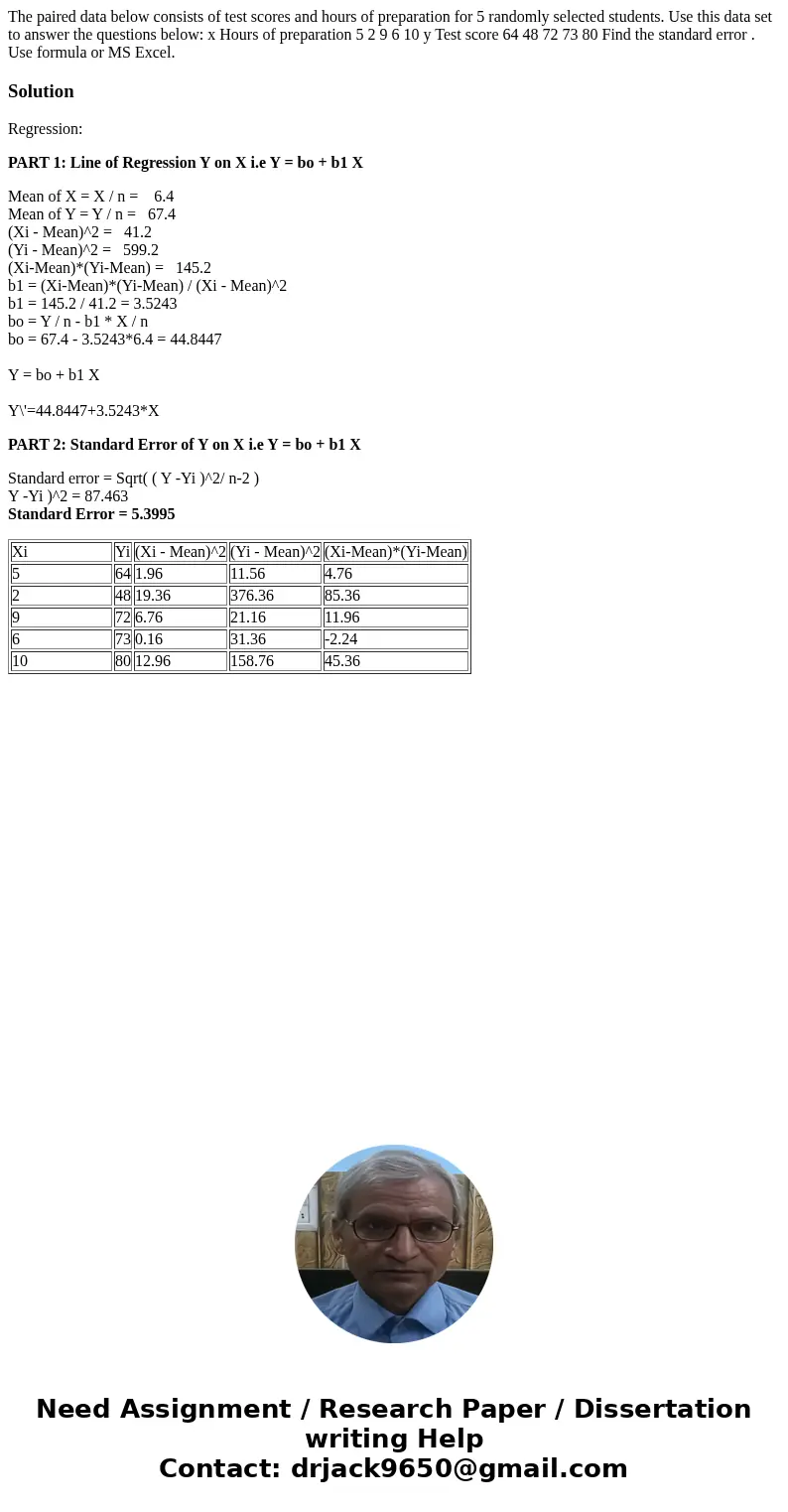
| Xi | Yi | (Xi - Mean)^2 | (Yi - Mean)^2 | (Xi-Mean)*(Yi-Mean) |
| 5 | 64 | 1.96 | 11.56 | 4.76 |
| 2 | 48 | 19.36 | 376.36 | 85.36 |
| 9 | 72 | 6.76 | 21.16 | 11.96 |
| 6 | 73 | 0.16 | 31.36 | -2.24 |
| 10 | 80 | 12.96 | 158.76 | 45.36 |
 Homework Sourse
Homework Sourse