intfracx10dx2x25x3Solution integral 10x35 x2 x2 dx Rewrite t

|int|frac(x+10)dx2x2+5x-3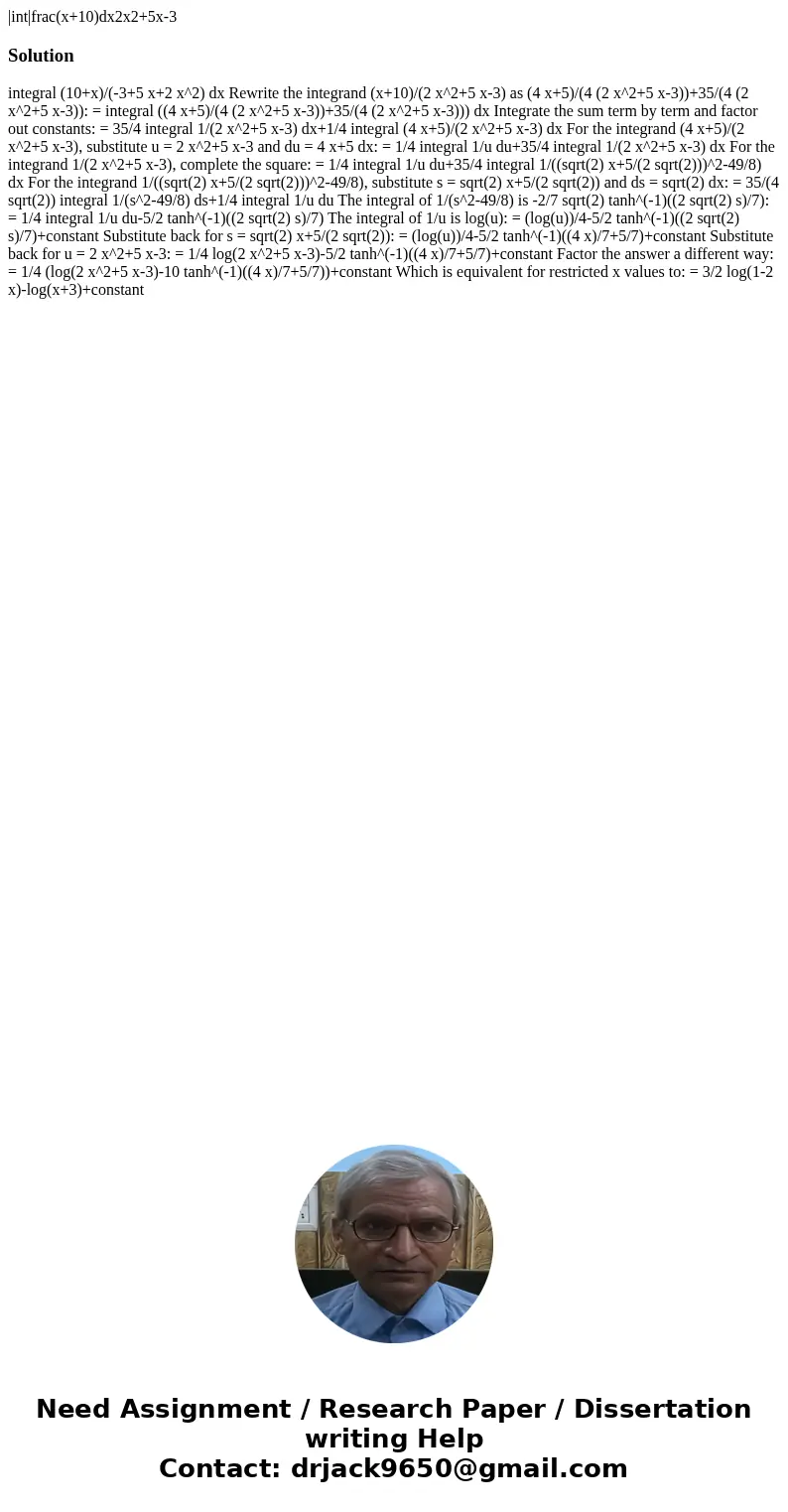

Solution

integral (10+x)/(-3+5 x+2 x^2) dx Rewrite the integrand (x+10)/(2 x^2+5 x-3) as (4 x+5)/(4 (2 x^2+5 x-3))+35/(4 (2 x^2+5 x-3)): = integral ((4 x+5)/(4 (2 x^2+5 x-3))+35/(4 (2 x^2+5 x-3))) dx Integrate the sum term by term and factor out constants: = 35/4 integral 1/(2 x^2+5 x-3) dx+1/4 integral (4 x+5)/(2 x^2+5 x-3) dx For the integrand (4 x+5)/(2 x^2+5 x-3), substitute u = 2 x^2+5 x-3 and du = 4 x+5 dx: = 1/4 integral 1/u du+35/4 integral 1/(2 x^2+5 x-3) dx For the integrand 1/(2 x^2+5 x-3), complete the square: = 1/4 integral 1/u du+35/4 integral 1/((sqrt(2) x+5/(2 sqrt(2)))^2-49/8) dx For the integrand 1/((sqrt(2) x+5/(2 sqrt(2)))^2-49/8), substitute s = sqrt(2) x+5/(2 sqrt(2)) and ds = sqrt(2) dx: = 35/(4 sqrt(2)) integral 1/(s^2-49/8) ds+1/4 integral 1/u du The integral of 1/(s^2-49/8) is -2/7 sqrt(2) tanh^(-1)((2 sqrt(2) s)/7): = 1/4 integral 1/u du-5/2 tanh^(-1)((2 sqrt(2) s)/7) The integral of 1/u is log(u): = (log(u))/4-5/2 tanh^(-1)((2 sqrt(2) s)/7)+constant Substitute back for s = sqrt(2) x+5/(2 sqrt(2)): = (log(u))/4-5/2 tanh^(-1)((4 x)/7+5/7)+constant Substitute back for u = 2 x^2+5 x-3: = 1/4 log(2 x^2+5 x-3)-5/2 tanh^(-1)((4 x)/7+5/7)+constant Factor the answer a different way: = 1/4 (log(2 x^2+5 x-3)-10 tanh^(-1)((4 x)/7+5/7))+constant Which is equivalent for restricted x values to: = 3/2 log(1-2 x)-log(x+3)+constant