1 Suppose there are two countries with 10 people each Countr
Solution
a)
i. Var for A=((1-1.9)^2+(1-1.9)^2+(1-1.9)^2+(1-1.9)^2+(1-1.9)^2+(1-1.9)^2+(1-1.9)^2+(1-1.9)^2+(1-1.9)^2+(10-1.9)^2)/10 = 7.29
var for B = ((1-2.8)^2+(1-2.8)^2+(1-2.8)^2+(1-2.8)^2+(1-2.8)^2+(1-2.8)^2+(1-2.8)^2+(1-2.8)^2+(10-2.8)^2+(10-2.8)^2)/10 = 12.96
ii. Coefficient of variation for A= (SD/mean)*100= (sqrt of var/mean)*100 = sqrt(7.29)/1.9 = 2.7/1.9 = 1.42
Coefficient of variation for B= (SD/mean)*100= (sqrt of var/mean)*100 = sqrt(12.96)/2.8 = 3.6/2.8 = 1.28
iii.the 80:20 ratio
for country A
80 percent of population earn 42.11 percent of income and 20 percent earn 57.89 percent of income
for country B
80 percent of population earn 28.57 percent of income and 20 percent earn 71.43 percent of income
iv the 90:20 ratio
for country A
90 percent of population earn 47.37 percent of income and 10 percent earn 52.63 percent of income
for country B
90 percent of population earn 64.29 percent of income and 10 percent earn 35.71 percent of income
b. Looking at the results, country A has more income inequality than country B
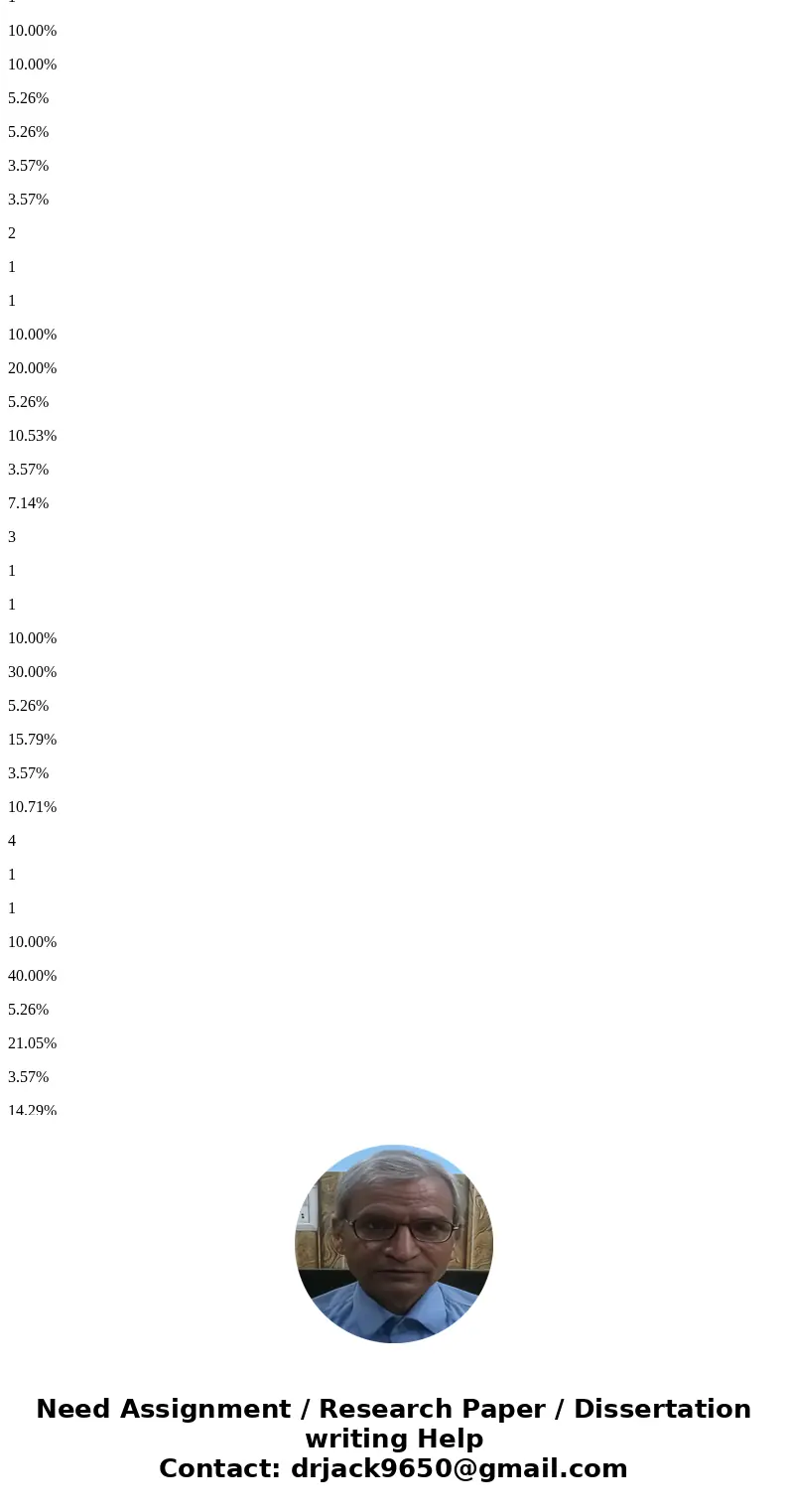
Citizens
A
B
Proportion of population (%)
Cumulative Proportion of population (%)
Income % of A
Cumulative Income % of A
Income % of B
Cumulative Income % of B
1
1
1
10.00%
10.00%
5.26%
5.26%
3.57%
3.57%
2
1
1
10.00%
20.00%
5.26%
10.53%
3.57%
7.14%
3
1
1
10.00%
30.00%
5.26%
15.79%
3.57%
10.71%
4
1
1
10.00%
40.00%
5.26%
21.05%
3.57%
14.29%
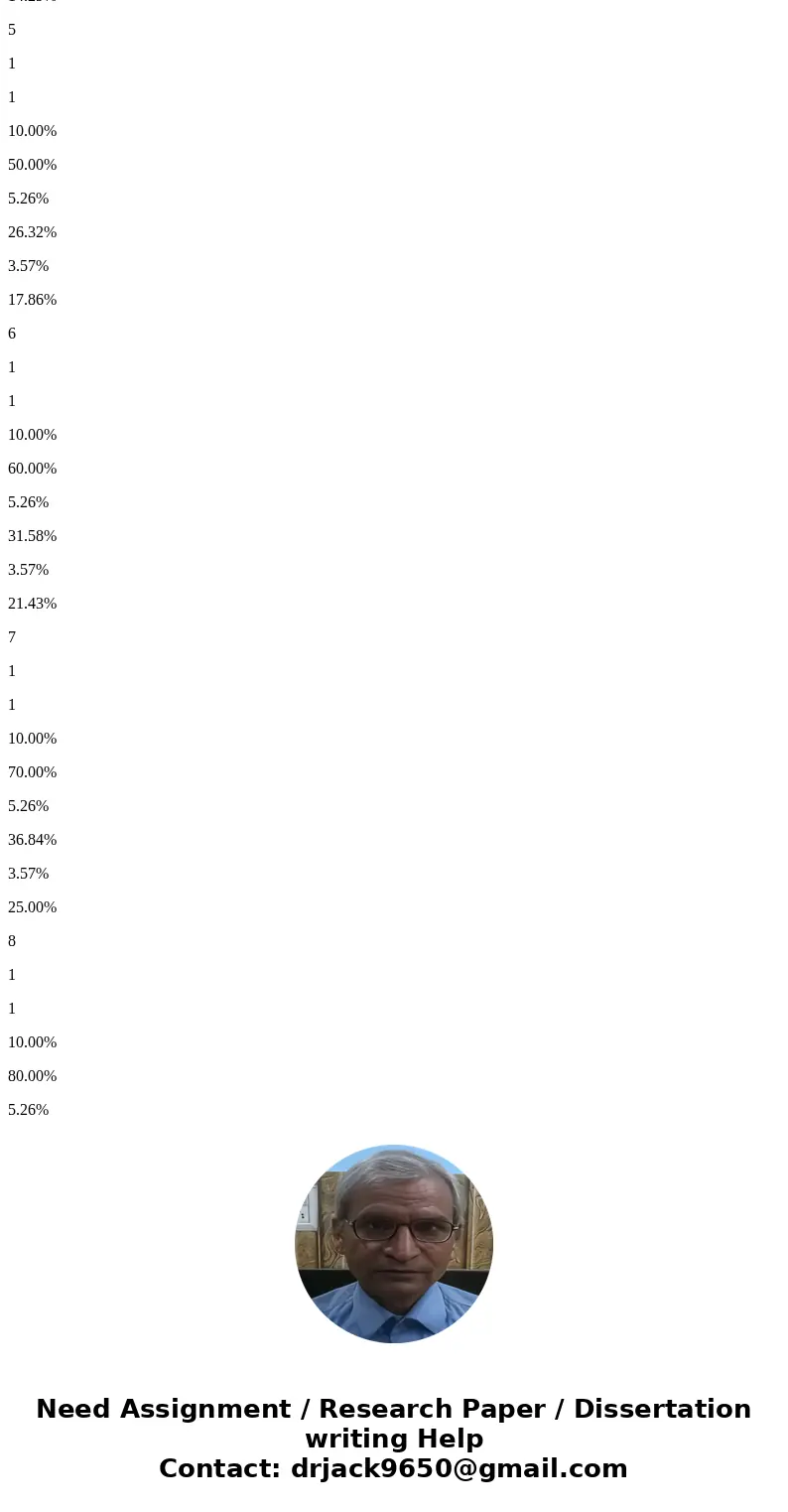
5
1
1
10.00%
50.00%
5.26%
26.32%
3.57%
17.86%
6
1
1
10.00%
60.00%
5.26%
31.58%
3.57%
21.43%
7
1
1
10.00%
70.00%
5.26%
36.84%
3.57%
25.00%
8
1
1
10.00%
80.00%
5.26%
42.11%
3.57%
28.57%
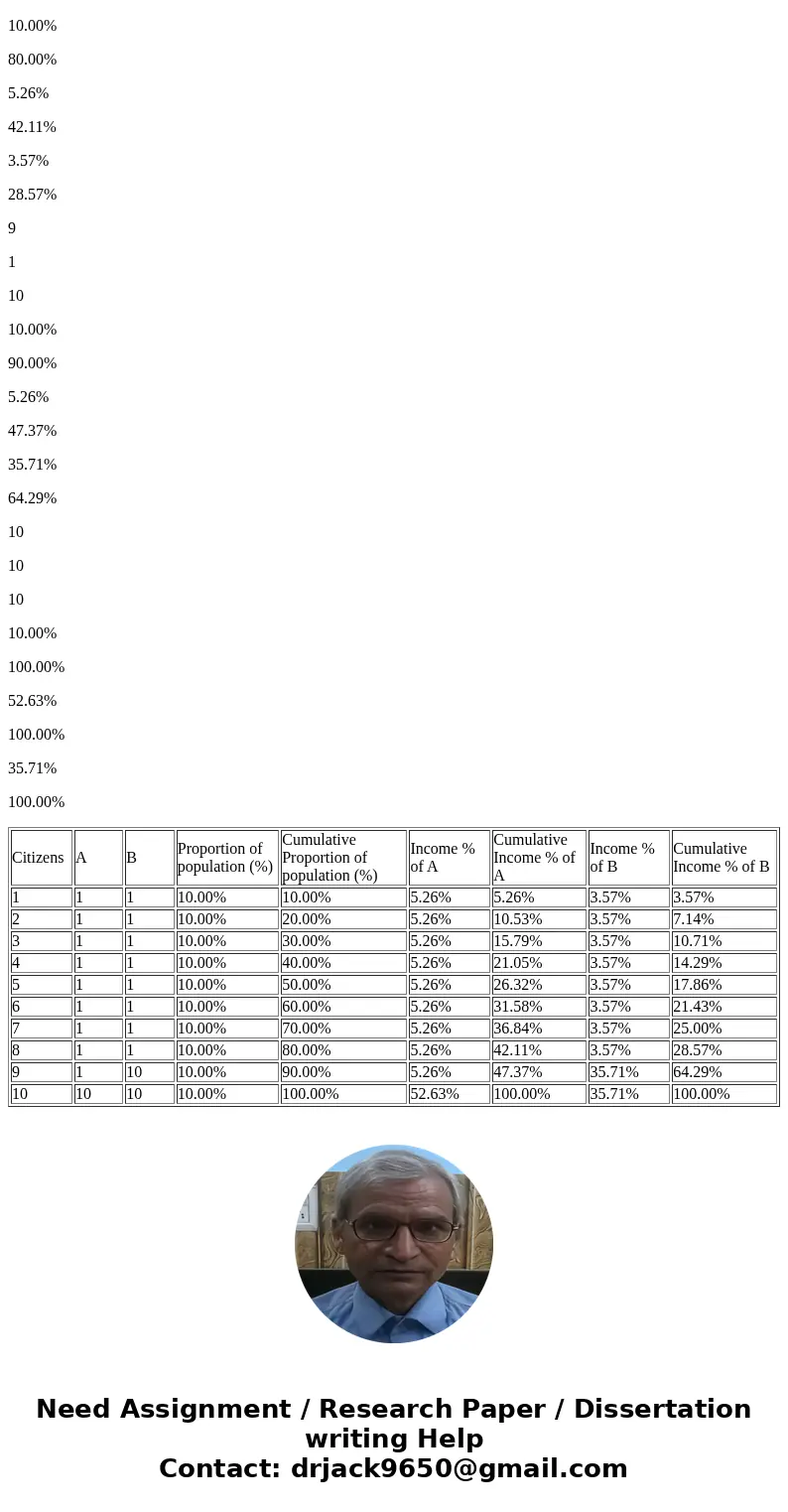
9
1
10
10.00%
90.00%
5.26%
47.37%
35.71%
64.29%
10
10
10
10.00%
100.00%
52.63%
100.00%
35.71%
100.00%
| Citizens | A | B | Proportion of population (%) | Cumulative Proportion of population (%) | Income % of A | Cumulative Income % of A | Income % of B | Cumulative Income % of B |
| 1 | 1 | 1 | 10.00% | 10.00% | 5.26% | 5.26% | 3.57% | 3.57% |
| 2 | 1 | 1 | 10.00% | 20.00% | 5.26% | 10.53% | 3.57% | 7.14% |
| 3 | 1 | 1 | 10.00% | 30.00% | 5.26% | 15.79% | 3.57% | 10.71% |
| 4 | 1 | 1 | 10.00% | 40.00% | 5.26% | 21.05% | 3.57% | 14.29% |
| 5 | 1 | 1 | 10.00% | 50.00% | 5.26% | 26.32% | 3.57% | 17.86% |
| 6 | 1 | 1 | 10.00% | 60.00% | 5.26% | 31.58% | 3.57% | 21.43% |
| 7 | 1 | 1 | 10.00% | 70.00% | 5.26% | 36.84% | 3.57% | 25.00% |
| 8 | 1 | 1 | 10.00% | 80.00% | 5.26% | 42.11% | 3.57% | 28.57% |
| 9 | 1 | 10 | 10.00% | 90.00% | 5.26% | 47.37% | 35.71% | 64.29% |
| 10 | 10 | 10 | 10.00% | 100.00% | 52.63% | 100.00% | 35.71% | 100.00% |

 Homework Sourse
Homework Sourse