Separated into 6 questions to make it worth your time 4 Whic
Separated into 6 questions to make it worth your time:
4) Which nation experiences the lowest level of income inequality?
Suppose you\'re an economist working for the Brookings Institute and you\'ve been asked to comment on what you see as a diverging level of inequality among representative households in two neighboring nations: Mira and Drovanna. You have the following information about these nations\' households for 2014 (income values in 2014 US dollar equivalencies) Mira Drovanna 16000 28000 11000 32000 900056000 18000 43000 15000 88000 126000 36000 22000 27000 31000 61000 10000 59000 12000 48000 The Brookings Institute is about to recommend one of these nations to the World Bank as a nation deserving of additional development funds due to its significant need to close its income gap, the other will be recognized for its relatively low level of income inequality.Solution
The income inequality in each country can be calculated with the help of Gini Coefficient from the given data.
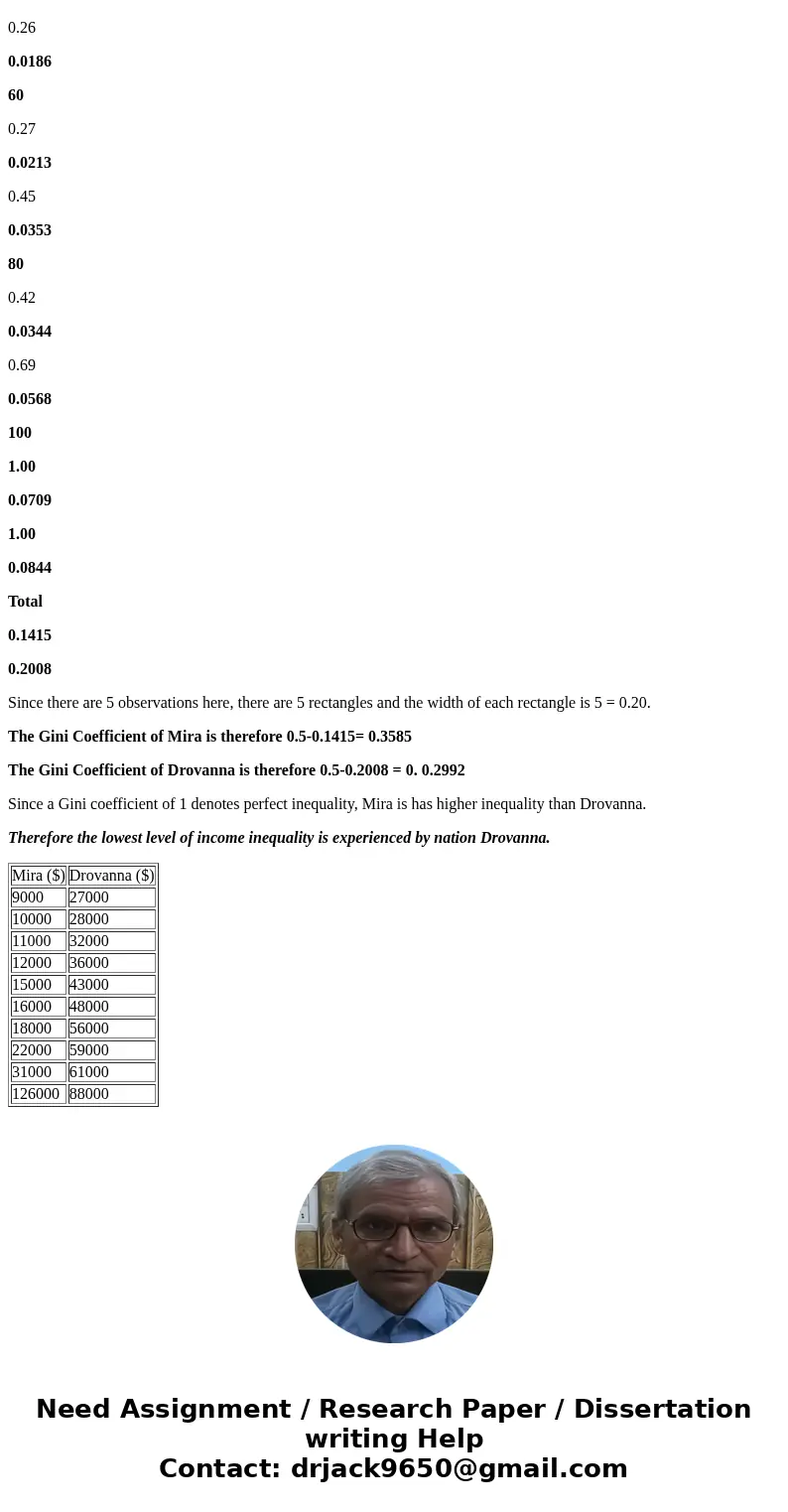
Mira ($)
Drovanna ($)
9000
27000
10000
28000
11000
32000
12000
36000
15000
43000
16000
48000
18000
56000
22000
59000
31000
61000
126000
88000
Quintile
Income of Mira ($)
Percentage of Mira’s income (%)
Cumulative % of Mira’s income (%)
Cumulative proportion of Mira’s income
Income of Drovanna ($)
Percentage of Drovanna’s income
Cumulative % of Drovanna’s income
Cumulative proportion of Drovanna’’s income
20
19000
7.04
7.04
70.4/100 = 0.07
55000
11.51
11.51
0.12
40
23000
8.52
15.56
0.16
68000
14.23
25.73
0.26
60
31000
11.48
27.04
0.27
91000
19.04
44.77
0.45
80
40000
14.81
41.85
0.42
115000
24.06
68.83
0.69
100
157000
58.15
100.00
1.00
149000
31.17
100.00
1.00
Total
270000
100.00
478000
100.00
If we find out the area lying below each country’s Lorenz curve, and subtract it from the area of the right angled triangle (0.5), then we can get the area lying within each country’s Lorenz curve. The Gini Coefficient for each country would then be the ratio of the area lying within each country’s Lorenz curve to the area of the triangle (0.5).
The calculations have been done in the table below.
It is important to note that for calculating the area below the Lorenz curve, if the whole curve is divided into rectangles, then the area of each rectangle equals the sum of its previous cumulative % of income and its own cumulative percentage of income, whole divided by 2, times the width of each rectangle. All these individual areas are summed to get the area under the Lorenz curve for each country.
Quintile
Cumulative proportion of Mira’s income
Area under the Lorenz Curve of Mira
Cumulative proportion of Drovanna’’s income
Area under the Lorenz Curve of Drovanna
0
0
0
0
0
20
0.07
[(0.07+0)/2]*0.10 = 0.0035
0.12
[(0.12+0)/2]*0.10
=
0.0058
40
0.16
0.0113
0.26
0.0186
60
0.27
0.0213
0.45
0.0353
80
0.42
0.0344
0.69
0.0568
100
1.00
0.0709
1.00
0.0844
Total
0.1415
0.2008
Since there are 5 observations here, there are 5 rectangles and the width of each rectangle is 5 = 0.20.
The Gini Coefficient of Mira is therefore 0.5-0.1415= 0.3585
The Gini Coefficient of Drovanna is therefore 0.5-0.2008 = 0. 0.2992
Since a Gini coefficient of 1 denotes perfect inequality, Mira is has higher inequality than Drovanna.
Therefore the lowest level of income inequality is experienced by nation Drovanna.
| Mira ($) | Drovanna ($) |
| 9000 | 27000 |
| 10000 | 28000 |
| 11000 | 32000 |
| 12000 | 36000 |
| 15000 | 43000 |
| 16000 | 48000 |
| 18000 | 56000 |
| 22000 | 59000 |
| 31000 | 61000 |
| 126000 | 88000 |




 Homework Sourse
Homework Sourse