Solve the following initial value problem x1 1 4 2 3x x0 0

Solve the following initial value problem. x^-1 = (1 4 2 3)x-, x-(0) = (0 3) x^-1 = (3 5 -2 1)x-, x-(243) = (5 14)

Solution

by seeing the matrix we have to solve these equation,

dx1 /dt = x1 + 4 x2

dx2 /dt = 2x1 + 3x2

now eigenvalues and eignvector corresponding to matrix

(1-r) (3-r) - 8 = 0

r = 5 or r = -1

corresponding to r = 5 ,eigenvector is (1 1)^T

corresponding to r = -1 , eigenvector is (-2 1 )^T

hence x = c1 (1 1)^T e^5t + c2 (-2 1 )^T e^-t

^{now seeing initial value we get}

c1 -2c2 = 0

c1 +c2 = 3

hence c1 = 2 ,c2 =1

hence x = 2 (1 1)^T    e^5t + (-2 1 )^T e^-t

b) similarly we can solve this part as in 1st part.

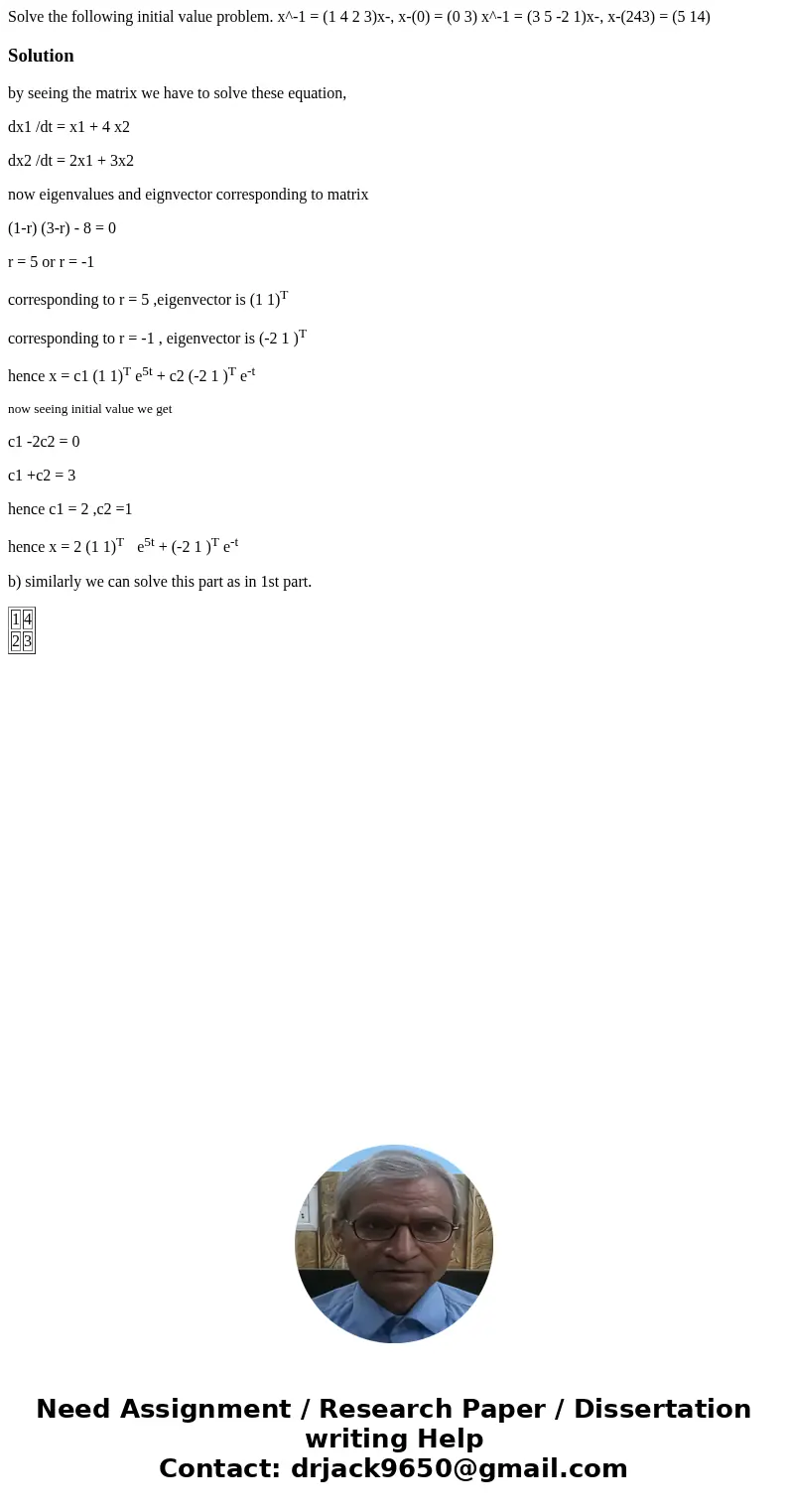
1	4
2	3