For this assignment you will use the statistical knowledge a

For this assignment, you will use the statistical knowledge and scientific writing skills acquired in this course to complete the Signature Assignment (Mock Study). Carefully review the information provided about the mock study, and then address each assignment requirement. You are the Director of Institutional Research at a small state university and you have been given the task of gathering information for the Dean of the School of Education regarding the performance of its undergraduate students on the Graduate Record Exam (GRE). Data on six variables were collected: gender, overall grade point average (GPA), major GPA, GRE scores in major area, GRE quantitative, GRE verbal, and type of preparation programs. The university is dedicated to maximizing student success on the GRE. The university has established five different options for students to prepare for the GREs: option 1 = completely online asynchronous prep course, 2 = completely online synchronous prep course, 3 = complete a hybrid prep course with a combination of online and face to face; 4 = complete a traditional instructor led prep course, and 5 = self-paced paper based prep course. The Dean has simply said to you, “Tell me what works best and for whom?” You decide to establish a pilot study with 50 randomly selected general science education seniors to determine the details of the methodology as well as to provide some initial data and corresponding results to learn if the research plan meets the Dean’s needs. The pilot study needs to contain the following components written in APA format: Part 1: Develop a clear purpose statement sentence capturing the essence of the intent of the pilot study. Develop a brief introduction including three research questions (with the use of corresponding symbols or Q1., Q2., Q3.) related to the purpose of the pilot study. For each of the three research questions, develop a null and alternative hypothesis (with the use of corresponding symbols or Ho1:, Ha1:, Ho2:, Ha2:, Ho3:, Ha3:). Using a statistical decision chart similar to Gragetter and Wallnau (2013) Chapter 19, select the appropriate statistical test/analysis for each research question. Briefly explain the choices for each research question. Conduct each analysis using SPSS on the SPSS data set developed in the Create a Mock Data Set in Week 7. The output of those tests should be placed in an Appendix for the final report to the Dean. Present and discuss the findings (as related to each research question and the fail to reject or rejection of each null hypothesis) in APA format. Part 2: Report appropriate descriptive results. Present the results in a logical fashion, answering the research questions and testing the hypotheses as stated and in an appropriate manner for the type of data collected. Identify the assumptions of statistical tests, explain the conducted tests to determine whether those assumptions were met, and discuss any violations of those assumptions. Make decisions based on the results of the statistical analysis, such as whether the results were statistically significant, and include relevant test statistics and p values. Refer to the APA Manual for guidance on how to present the results in the text, tables, and/or figures. Present sufficient information so the Dean can make independent judgments about the findings.

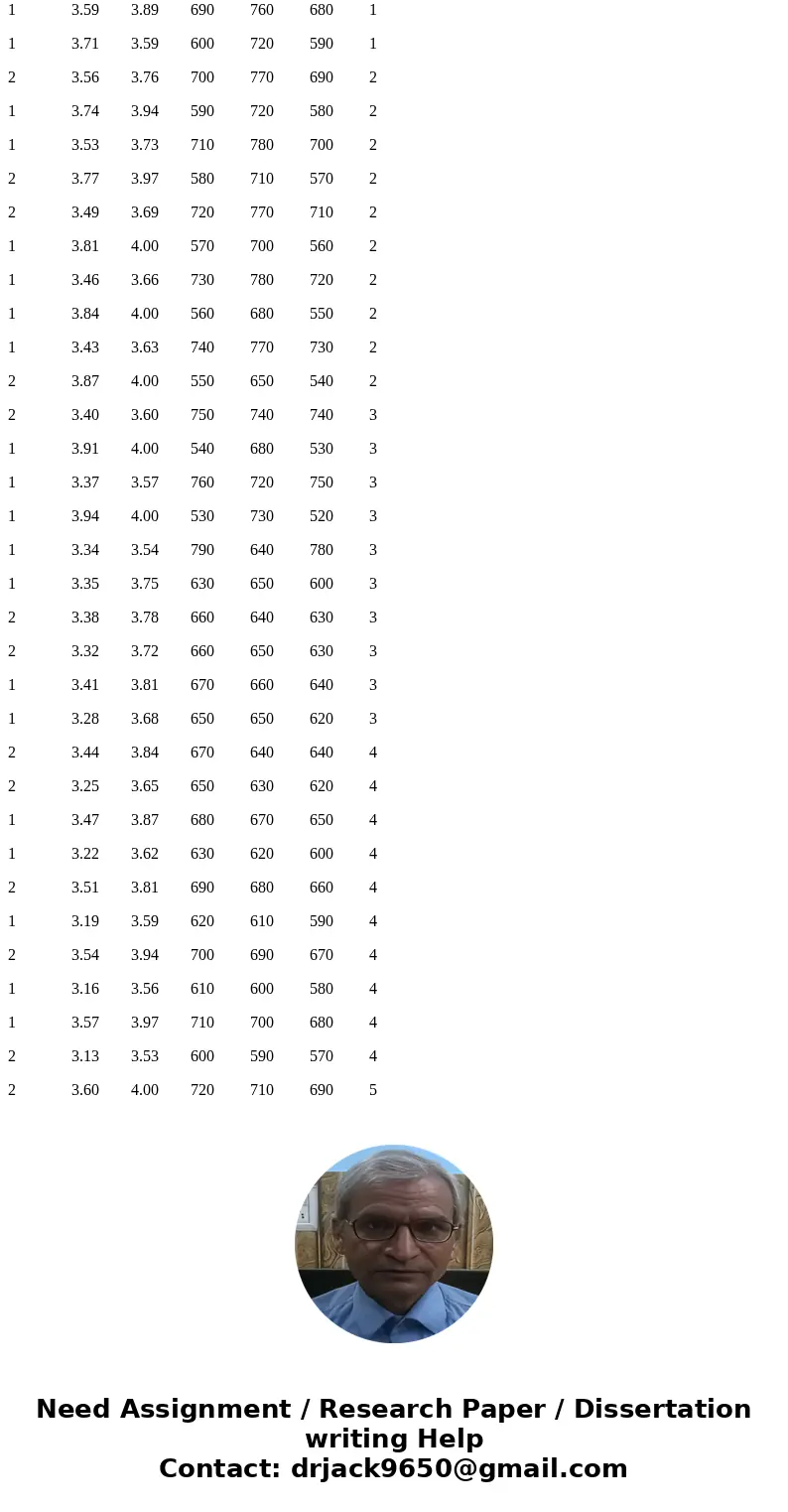
In this mock data file there are 50 participants and 6 variables:  

Variable column 1: Gender 1=male, 2=female

Variable column 2: overall grade point average (gpa) based on a 4 point system

Variable column 3: major gpa based on a 4 point system

Variable column 4; Graduate Record Exam (GRE) in major

Variable column 5; GRE quantitative

Variable column 6: GRE verbal

Variable column 7: Preparation Approach

**********************************************************************************

2              3.65        3.85        650         750         640         1

1              3.62        3.82        640         740         630         1             

1              3.68        3.88        660         760         650         1

1              3.59        3.79        630         750         620         1

1              3.71        3.91        670         740         660         1

2              3.65        3.85        620         760         610         1

1              3.62        3.82        680         750         670         1

1              3.68        3.88        610         740         600         1

1              3.59        3.89        690         760         680         1

1              3.71        3.59        600         720         590         1

2              3.56        3.76        700         770         690         2

1              3.74        3.94        590         720         580         2

1              3.53        3.73        710         780         700         2

2              3.77        3.97        580         710         570         2

2              3.49        3.69        720         770         710         2

1              3.81        4.00        570         700         560         2

1              3.46        3.66        730         780         720         2

1              3.84        4.00        560         680         550         2

1              3.43        3.63        740         770         730         2

2              3.87        4.00        550         650         540         2

2              3.40        3.60        750         740         740         3

1              3.91        4.00        540         680         530         3

1              3.37        3.57        760         720         750         3

1              3.94        4.00        530         730         520         3

1              3.34        3.54        790         640         780         3

1              3.35        3.75        630         650         600         3

2              3.38        3.78        660         640         630         3

2              3.32        3.72        660         650         630         3

1              3.41        3.81        670         660         640         3

1              3.28        3.68        650         650         620         3

2              3.44        3.84        670         640         640         4

2              3.25        3.65        650         630         620         4

1              3.47        3.87        680         670         650         4

1              3.22        3.62        630         620         600         4

2              3.51        3.81        690         680         660         4

1              3.19        3.59        620         610         590         4

2              3.54        3.94        700         690         670         4

1              3.16        3.56        610         600         580         4

1              3.57        3.97        710         700         680         4

2              3.13        3.53        600         590         570         4

2              3.60        4.00        720         710         690         5

1              3.10        3.50        590         570         560         5

1              3.63        4.00        730         680         700         5

1              3.00        3.40        580         550         550         5

1              3.71        4.00        750         730         720         5

2              2.90        3.30        560         580         530         5

2              3.81        4.00        760         630         730         5

1              2.80        3.20        530         670         470         5

1              3.91        4.00        770         560         740         5

2              3.86        4.00        520         600         490         5

Question 1; Do males or females score higher on the GRE quantitative section?

Question 2: Do males or females score higher on the GRE verbal section?

Question 3: Do males or females have a more successful preparation approach?

Solution

Q1.

Ho1: Males and Females score equal on GRE quantitative section, i.e, _m - _f = 0

Ha1: Males score higher than females on GRE quantitative section, i.e., _m - _f > 0

or Ha1: Females score higher than males on GRE quantitative section, i.e., _m - _f < 0

The test statistic is a t-score (t) defined by the following equation.

t = [ mean(x₁) - mean(x₂) - 0 ] / SE

SE = sqrt[ ((n₁-1)s₁² + (n₂-1)s₂²⁾/(n₁+n₂-2) ]* sqrt[(1/n₁) + (1/n₂)] (1 is for male population, 2 is for female)

Here,

n₁= 32, n₂=18, mean(x₁)=690 mean(x₂)=677.22 s₁²= 4232.26 s₂²= 3962.42

SE= sqrt[((4232.26*31) + (3962.42*17))/48 ]* sqrt[(1/32) + (1/18)]=18.95

t = (690 - 677.22)/18.95 = 0.67

t₄₈(0.05)= 1.96

since, t < t₄₈(0.05), we fail to reject Ho1.

Hence, Males and Females score equal on GRE quantitative section

Q2.

Ho2: Males and Females score equal on GRE verbal section, i.e, _m - _f = 0

Ha2: Males score higher than females on GRE verbal section, i.e., _m - _f > 0

or Ha1: Females score higher than males on GRE verbal section, i.e., _m - _f < 0

The test statistic is a t-score (t) defined by the following equation.

t = [ mean(x₁) - mean(x₂) - 0 ] / SE

SE = sqrt[ ((n₁-1)s₁² + (n₂-1)s₂²⁾/(n₁+n₂-2) ]* sqrt[(1/n₁) + (1/n₂)]  (1 is for male population, 2 is for female)

Here,

n₁= 32, n₂=18, mean(x₁)=631.86 mean(x₂)=631.11 s₁²= 5635.08.26 s₂²= 4928.11

SE= sqrt[((5635.08*31) + (4928.11*17))/48 ]* sqrt[(1/32) + (1/18)]=21.62

t = (631.86 - 631.11)/21.62 = 0.03

t₄₈(0.05)= 1.96

since, t < t₄₈(0.05), we fail to reject Ho2.

Hence, Males and Females score equal on GRE verbal section

Q3. Testing different approaches on males and females (using overall GRE scores, i.e., variable 2)

Ho3: Males and Females score equal using approach i, i.e, _m - _f = 0

Ha3: Males score higher than females using approach i, i.e., _m - _f > 0

or Ha1: Females score higher than males using approach i, i.e., _m - _f < 0 (i = 1,2,3,4,5)

The test statistic is a t-score (t) defined by the following equation.

t = [ mean(x₁) - mean(x₂) - 0 ] / SE

SE = sqrt[ ((n₁-1)s₁² + (n₂-1)s₂²⁾/(n₁+n₂-2) ]* sqrt[(1/n₁) + (1/n₂)]  (1 is for male population, 2 is for female)

Approach 1

n₁= 8, n₂=2, mean(x₁)=3.65 mean(x₂)=3.65 s₁²= 0.0026 s₂²= 0

SE= sqrt[((0.0026*7) + (0)/8) ]* sqrt[(1/8) + (1/2)]=0.0152

t = (3.65-3.65)/0.0152 = 0

t₈(0.05)= 1.86

since, t < t₈(0.05), we fail to reject Ho3.

Hence, Males and Females score equal using Approach 1.

Approach 2

n₁= 6, n₂=4, mean(x₁)=3.64 mean(x₂)=3.67 s₁²= 0.0335 s₂²= 0.0315

SE= sqrt[((0.0335*5) + (0.0315*3))/8 ]* sqrt[(1/6) + (1/4)]=0.0761

t = (3.64-3.67)/0.0761 = -0.39

t₈(0.05)= 1.86

since, t > -t₈(0.05), we fail to reject Ho3.

Hence, Males and Females score equal using Approach 2.

Approach 3

n₁= 7, n₂=3, mean(x₁)=3.51 mean(x₂)=3.37 s₁²= 0.0803 s₂²= 0.0018

SE= sqrt[((0.0803*6) + (0.0018/2))/8 ]* sqrt[(1/7) + (1/3)]=0.167

t = (3.51-3.37)/0.167 = 0.84

t₈(0.05)= 1.86

since, t < t₈(0.05), we fail to reject Ho3.

Hence, Males and Females score equal using Approach 3.

Approach 4

n₁= 5, n₂=5, mean(x₁)=3.32 mean(x₂)=3.38 s₁²= 0.0344 s₂²= 0.0314

SE= sqrt[((0.0344*4) + (0.0314*4))/8 ]* sqrt[(1/5) + (1/5)]=0.1147

t = (3.32-3.38)/0.1157 = -0.52

t₈(0.05)= 1.86

since, t > -t₈(0.05), we fail to reject Ho3.

Hence, Males and Females score equal using Approach 4.

Approach 5

n₁= 6, n₂=4, mean(x₁)=3.56 mean(x₂)=3.54 s₁²= 0.2505 s₂²= 0.1962

SE= sqrt[((0.2505*5) + (0.1962*3))/8 ]* sqrt[(1/6) + (1/4)]=0.3097

t = (3.56-3.54)/0.3097 = 0.06

t₈(0.05)= 1.86

since, t < t₈(0.05), we fail to reject Ho3.

Hence, Males and Females score equal using Approach 5.

No, Males and females score equally using all the approaches