FW Incorporated is a company that produces four different ty

FW Incorporated is a company that produces four different types of furniture items. Each of these products passes through five production steps before being ready for distribution: drilling, painting, assembling, cleaning, and packaging. FW has collected the information given in Table 1 about the total number of hours required for one unit of each product to go though each production step. For example, one unit of product 1 requires 0.03 hours of drilling (note that product 3 does not require painting). The total number of hours dedicated for each production step cannot exceed the bound given in Table 1. For example, the total number of hours used for drilling on all the products cannot be more than 400. Furthermore, during the assembly process, products 2 and 4 need a special glue that comes in the form of plastic sheets. Product 2 requires 2.0 ft2 of the special glue per unit produced, whereas Product 4 needs 1.4 ft2 . The company has only 2000 ft2 of glue available for the assembly process. The marketing team at FW used historical data to generate a detailed forecast of the demand of each product. The team observed that the demand always falls between a range as indicated in Table 2. In other words, according to the data, there is a minimum amount of product that FW is guaranteed to sell, but there is also a limit on the number of items FW expects to sell. Any production beyond that will most likely remain unsold and wasted. In addition to the forecast for the demand, Table 2 also presents both the selling price and production cost per unit for each product type. FW wants to know how many units of each product must be produced guaranteeing that all the conditions are satisfied. Answer the following problems:

Production rate Ste Drillin Paintin Assemblin Cleanin uct 2 0.15 0.12 0.10 0.20 0.06 duct 4 Hours available 0.10 0.10 0.12 0.12 0.12 uct 0.05 0.03 0.06 0.05 0.04 0.02 0.05 0.03 0.02 400 400 500 450 Packa Table 1: Production information Potential demand ProductSell price / unitProduction cost / unit um aximurn 10 25 1,000 6,000 15 3,000 1,000 4 20 14 100 Table 2: Marketing information 1. (5 points) Provide an explicit formulation for this problem. An explicit formulation is one that is described term by term. e.g., the formulation for the oil problem we covered in class. In this example, we have expressions like 0.3x1 + 0.4x2 2000 2. (10 points) Provide a general formulation for this problem specifying:s (a) Sets (b) Parameters (c) Decision variables (d) Constraints (e) Objective function For example, a general formulation is one like the last version of the production/distribution problem we covered in class. 3. (5 points) Solve the problem using the MS Excel solver 4. (5 points) Given the solution obtained by the solver, analyze the results. Provide insights about the production levels and the usage of the production steps. 5. (5 points) Analyze the change in the optimal solution if the number of drilling hours increases by 200. How much will you be willing to pay for having these extra hours?

Solution

3. Let the number of units of each product of type 1,2,3,4 be \"a\", \"b\", \"c\", \"d\" respectively.

The objective is to maximize profit (revenue - costs)

profit of product 1 = 10a-6a = 4a

profit of product 2 = 25b-15b = 10b

profit of product 3 = 16c-11c = 5c

profit of product 4 = 20d-14d = 6d

Total profits = 4a+10b+5c+6d. This is the objective function and has to be maximized.

Constraints are;

1. 0.03a+0.15b+0.05c+0.10d<=400

2. 0.06a+0.12b+0.10d<=400

3. 0.05a+0.10b+0.05c+0.12d<=500

4. 0.04a+0.2b+0.03c+0.12d<=450

5. 0.02a+0.06b+0.02c+0.12d<= 400

(hours availabe constraints are constraints 1 to 5 above)

6. 2b+1.4d<=2000 (glue available)

7. a should be greater than equal to 1000 and less than equal to 6,000.

8. b should be greater than equal to 0 and less than equal to 500

9. c should be greater than equal to 500 and less than equal to 3,000

10. d should be greater than equal to 100 and less than equal to 1,000

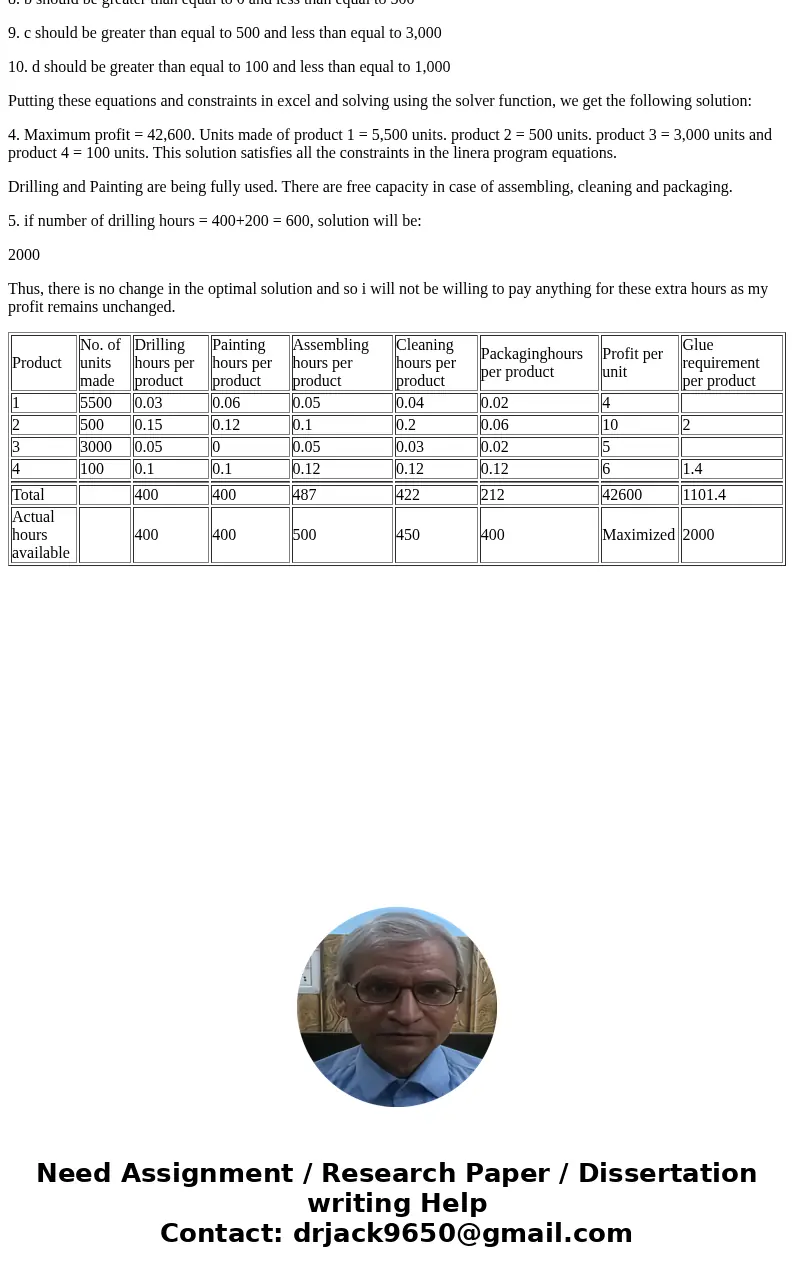
Putting these equations and constraints in excel and solving using the solver function, we get the following solution:

4. Maximum profit = 42,600. Units made of product 1 = 5,500 units. product 2 = 500 units. product 3 = 3,000 units and product 4 = 100 units. This solution satisfies all the constraints in the linera program equations.

Drilling and Painting are being fully used. There are free capacity in case of assembling, cleaning and packaging.

5. if number of drilling hours = 400+200 = 600, solution will be:

2000

Thus, there is no change in the optimal solution and so i will not be willing to pay anything for these extra hours as my profit remains unchanged.

Product	No. of units made	Drilling hours per product	Painting hours per product	Assembling hours per product	Cleaning hours per product	Packaginghours per product	Profit per unit	Glue requirement per product
1	5500	0.03	0.06	0.05	0.04	0.02	4
2	500	0.15	0.12	0.1	0.2	0.06	10	2
3	3000	0.05	0	0.05	0.03	0.02	5
4	100	0.1	0.1	0.12	0.12	0.12	6	1.4
Total		400	400	487	422	212	42600	1101.4
Actual hours available		400	400	500	450	400	Maximized	2000