X d2 y 2x5 dd Solution Solve the Bernoulli equation x dy

X d2 + y = _ 2x5+. d-d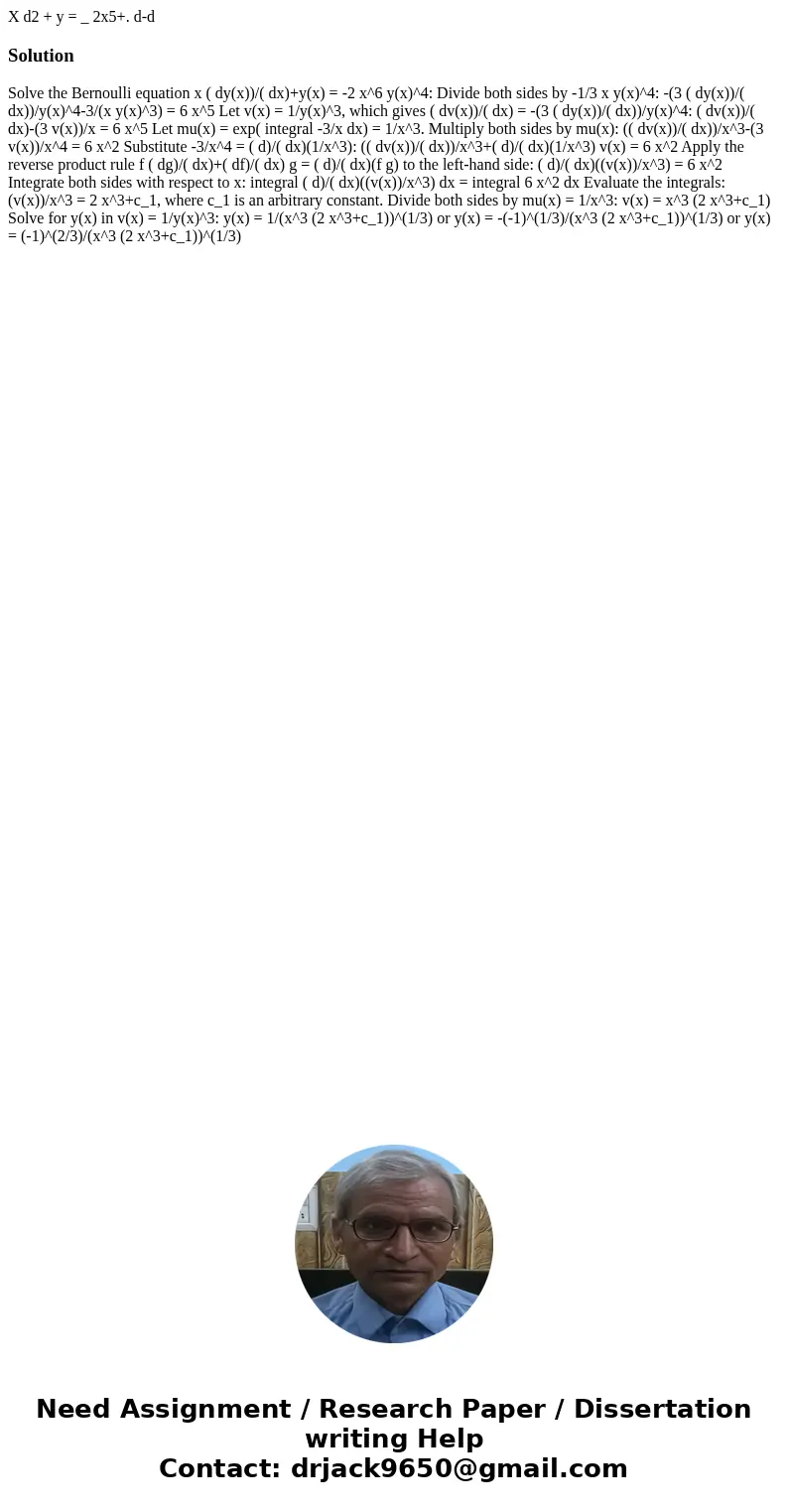

Solution

Solve the Bernoulli equation x ( dy(x))/( dx)+y(x) = -2 x^6 y(x)^4: Divide both sides by -1/3 x y(x)^4: -(3 ( dy(x))/( dx))/y(x)^4-3/(x y(x)^3) = 6 x^5 Let v(x) = 1/y(x)^3, which gives ( dv(x))/( dx) = -(3 ( dy(x))/( dx))/y(x)^4: ( dv(x))/( dx)-(3 v(x))/x = 6 x^5 Let mu(x) = exp( integral -3/x dx) = 1/x^3. Multiply both sides by mu(x): (( dv(x))/( dx))/x^3-(3 v(x))/x^4 = 6 x^2 Substitute -3/x^4 = ( d)/( dx)(1/x^3): (( dv(x))/( dx))/x^3+( d)/( dx)(1/x^3) v(x) = 6 x^2 Apply the reverse product rule f ( dg)/( dx)+( df)/( dx) g = ( d)/( dx)(f g) to the left-hand side: ( d)/( dx)((v(x))/x^3) = 6 x^2 Integrate both sides with respect to x: integral ( d)/( dx)((v(x))/x^3) dx = integral 6 x^2 dx Evaluate the integrals: (v(x))/x^3 = 2 x^3+c_1, where c_1 is an arbitrary constant. Divide both sides by mu(x) = 1/x^3: v(x) = x^3 (2 x^3+c_1) Solve for y(x) in v(x) = 1/y(x)^3: y(x) = 1/(x^3 (2 x^3+c_1))^(1/3) or y(x) = -(-1)^(1/3)/(x^3 (2 x^3+c_1))^(1/3) or y(x) = (-1)^(2/3)/(x^3 (2 x^3+c_1))^(1/3)