Find a linearly independent set of vectors that spans the sa

Find a linearly independent set of vectors that spans the same subspace of R^3 as that spanned by the vectors

V={(-3,-6,3),(-2,-1,-1),(-1,-1,0)}

Solution

Answer Procedure

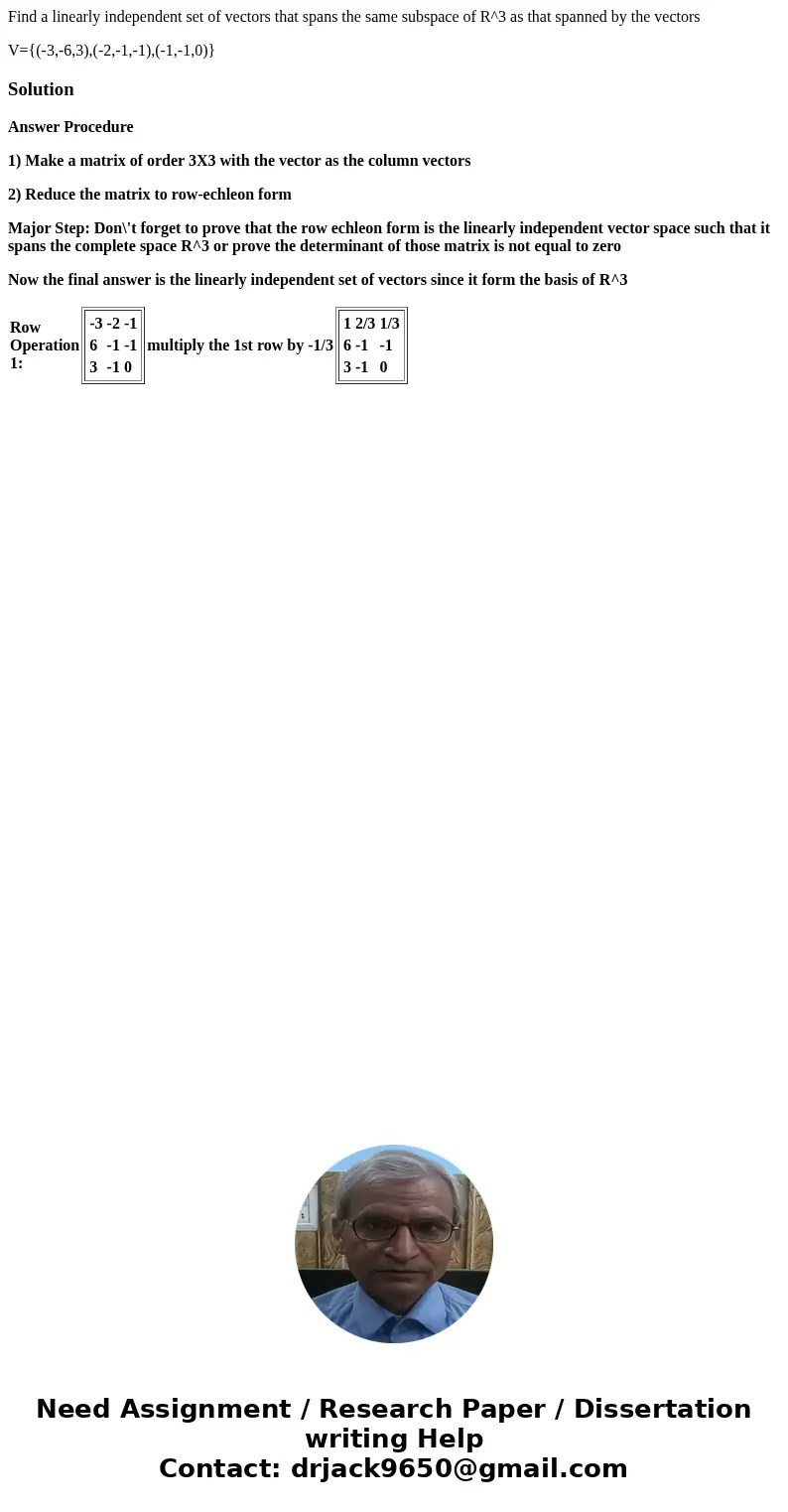
1) Make a matrix of order 3X3 with the vector as the column vectors

2) Reduce the matrix to row-echleon form

Major Step: Don\'t forget to prove that the row echleon form is the linearly independent vector space such that it spans the complete space R^3 or prove the determinant of those matrix is not equal to zero

Now the final answer is the linearly independent set of vectors since it form the basis of R^3