Homework SourseFor the data set A Find the multiple regression line Y B0
For the data set:
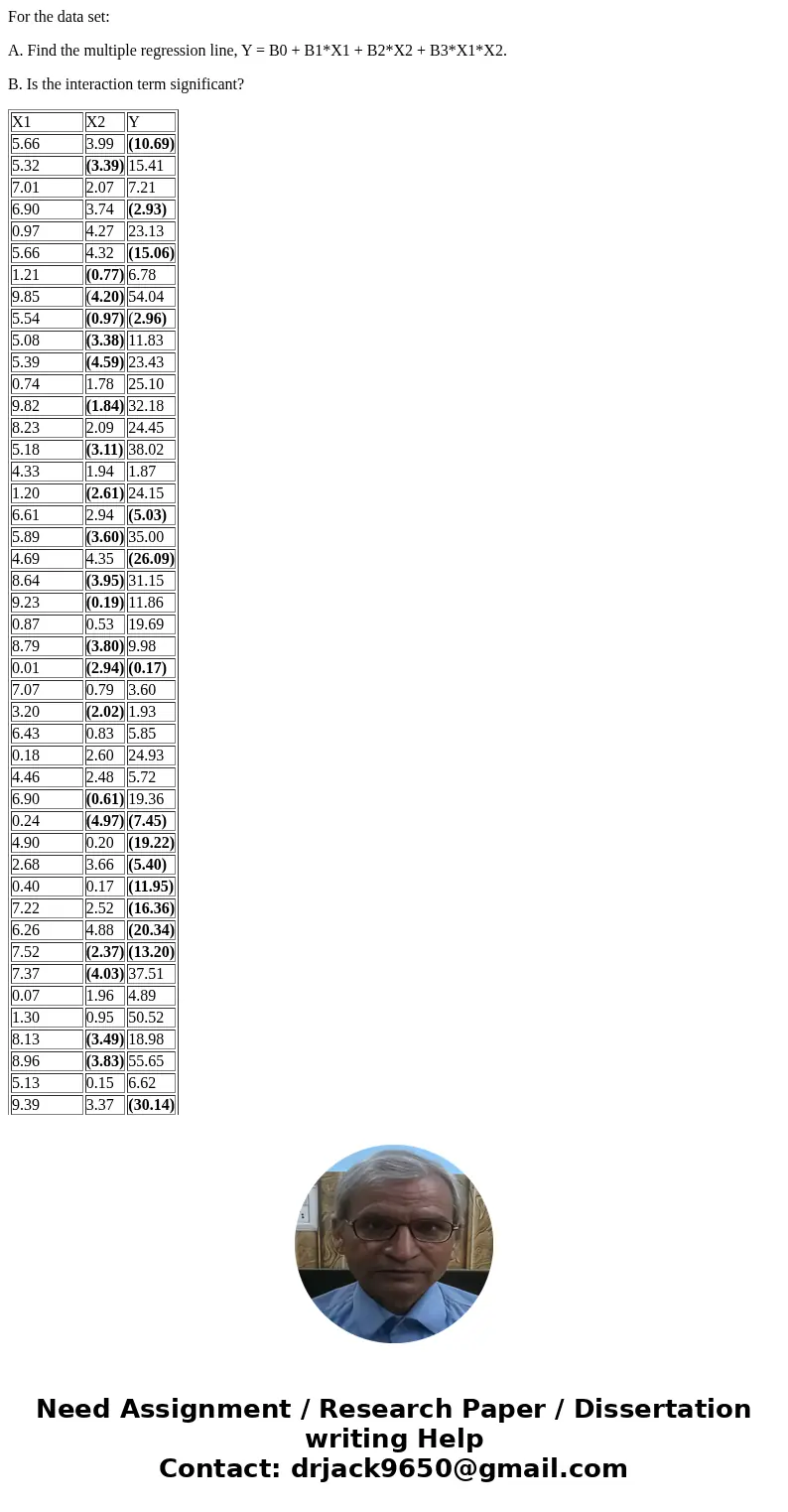
A. Find the multiple regression line, Y = B0 + B1*X1 + B2*X2 + B3*X1*X2.
B. Is the interaction term significant?
| X1 | X2 | Y |
| 5.66 | 3.99 | (10.69) |
| 5.32 | (3.39) | 15.41 |
| 7.01 | 2.07 | 7.21 |
| 6.90 | 3.74 | (2.93) |
| 0.97 | 4.27 | 23.13 |
| 5.66 | 4.32 | (15.06) |
| 1.21 | (0.77) | 6.78 |
| 9.85 | (4.20) | 54.04 |
| 5.54 | (0.97) | (2.96) |
| 5.08 | (3.38) | 11.83 |
| 5.39 | (4.59) | 23.43 |
| 0.74 | 1.78 | 25.10 |
| 9.82 | (1.84) | 32.18 |
| 8.23 | 2.09 | 24.45 |
| 5.18 | (3.11) | 38.02 |
| 4.33 | 1.94 | 1.87 |
| 1.20 | (2.61) | 24.15 |
| 6.61 | 2.94 | (5.03) |
| 5.89 | (3.60) | 35.00 |
| 4.69 | 4.35 | (26.09) |
| 8.64 | (3.95) | 31.15 |
| 9.23 | (0.19) | 11.86 |
| 0.87 | 0.53 | 19.69 |
| 8.79 | (3.80) | 9.98 |
| 0.01 | (2.94) | (0.17) |
| 7.07 | 0.79 | 3.60 |
| 3.20 | (2.02) | 1.93 |
| 6.43 | 0.83 | 5.85 |
| 0.18 | 2.60 | 24.93 |
| 4.46 | 2.48 | 5.72 |
| 6.90 | (0.61) | 19.36 |
| 0.24 | (4.97) | (7.45) |
| 4.90 | 0.20 | (19.22) |
| 2.68 | 3.66 | (5.40) |
| 0.40 | 0.17 | (11.95) |
| 7.22 | 2.52 | (16.36) |
| 6.26 | 4.88 | (20.34) |
| 7.52 | (2.37) | (13.20) |
| 7.37 | (4.03) | 37.51 |
| 0.07 | 1.96 | 4.89 |
| 1.30 | 0.95 | 50.52 |
| 8.13 | (3.49) | 18.98 |
| 8.96 | (3.83) | 55.65 |
| 5.13 | 0.15 | 6.62 |
| 9.39 | 3.37 | (30.14) |
| 0.75 | 2.23 | 17.68 |
| 1.46 | (1.47) | 28.36 |
| 3.95 | (0.42) | 10.17 |
| 1.76 | (4.42) | (0.98) |
| 5.75 | 2.24 | (14.38) |
Solution
Running this regression in SPSS, we get the following regression table
Coefficients(a)
Unstandardized Coefficients Standardized Coefficients
Model B Std. Error Beta t Sig
(Constant) 22.714 6.459 3.516 .001
X1 -2.194 1.229 -.485 -1.785 .081
X2 -4.206 2.345 -.441 -1.794 .079
X12 1.258 .422 1.084 2.981 .005
a. Dependent Variable: Y
From above table, regression line is Y=22.714 - 2.194 X1 - 4.206 X2 + 1.258 X1X2
We see that the p value for interaction effect is 0.005 which is less than 0.05, so we reject the null hypothesis that coefficient is insignificant and accept the alternative that interaction effect is significant.
Interaction term is significant.
