If Melinda buys 2 tickets to the raffle in exercise 19 what
If Melinda buys 2 tickets to the raffle in exercise 19, what is her expectation? (#19: Melinda buys (1) raffle ticket at the spring fling since there is (1) 1,000 prize, (1) $500 prize, and (5) $100 prizes. There were a total of 1,000 tickets sold at $3.00 each. What is Melinda\'s expectation?
Solution
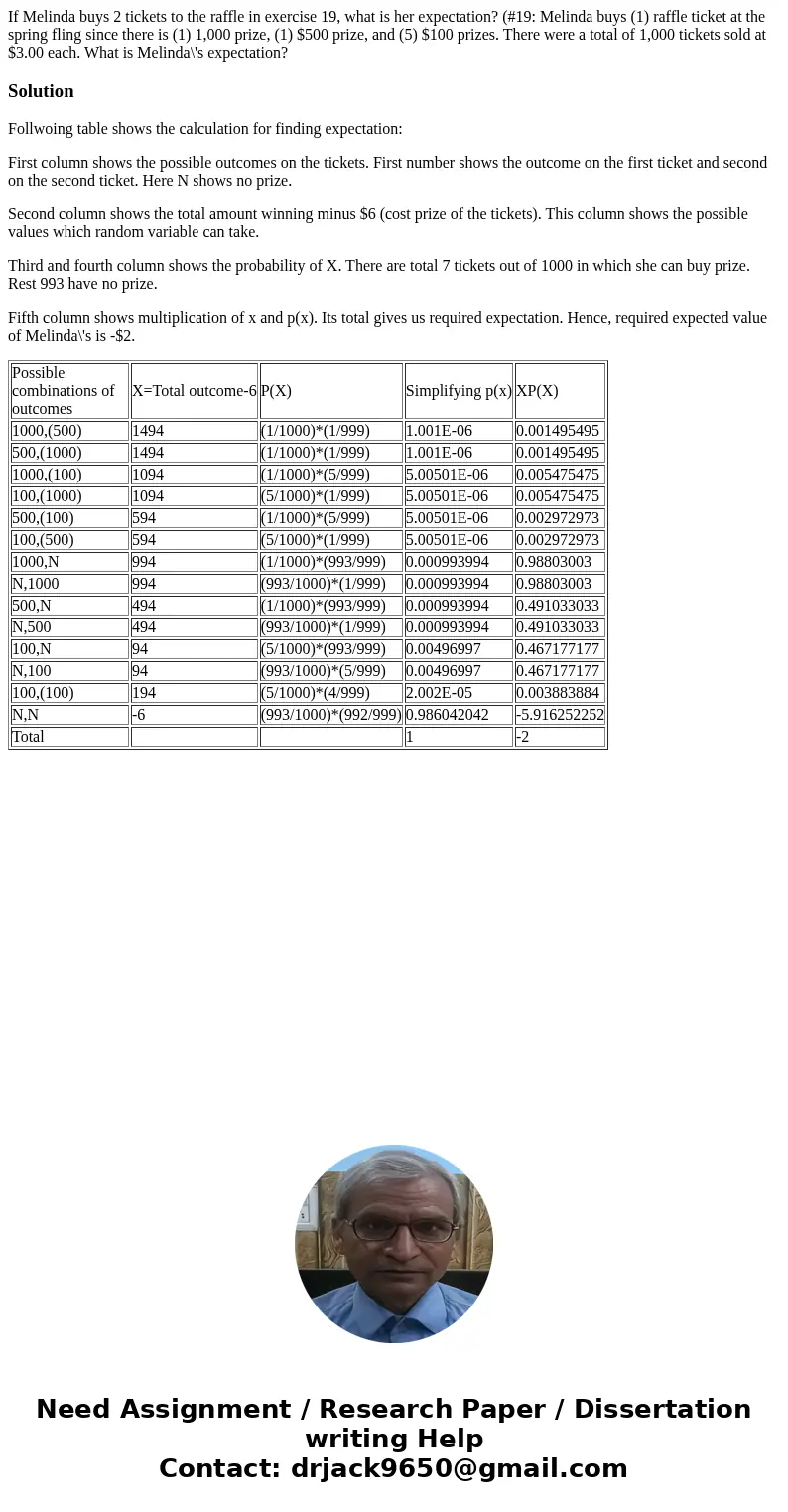
Follwoing table shows the calculation for finding expectation:
First column shows the possible outcomes on the tickets. First number shows the outcome on the first ticket and second on the second ticket. Here N shows no prize.
Second column shows the total amount winning minus $6 (cost prize of the tickets). This column shows the possible values which random variable can take.
Third and fourth column shows the probability of X. There are total 7 tickets out of 1000 in which she can buy prize. Rest 993 have no prize.
Fifth column shows multiplication of x and p(x). Its total gives us required expectation. Hence, required expected value of Melinda\'s is -$2.
| Possible combinations of outcomes | X=Total outcome-6 | P(X) | Simplifying p(x) | XP(X) |
| 1000,(500) | 1494 | (1/1000)*(1/999) | 1.001E-06 | 0.001495495 |
| 500,(1000) | 1494 | (1/1000)*(1/999) | 1.001E-06 | 0.001495495 |
| 1000,(100) | 1094 | (1/1000)*(5/999) | 5.00501E-06 | 0.005475475 |
| 100,(1000) | 1094 | (5/1000)*(1/999) | 5.00501E-06 | 0.005475475 |
| 500,(100) | 594 | (1/1000)*(5/999) | 5.00501E-06 | 0.002972973 |
| 100,(500) | 594 | (5/1000)*(1/999) | 5.00501E-06 | 0.002972973 |
| 1000,N | 994 | (1/1000)*(993/999) | 0.000993994 | 0.98803003 |
| N,1000 | 994 | (993/1000)*(1/999) | 0.000993994 | 0.98803003 |
| 500,N | 494 | (1/1000)*(993/999) | 0.000993994 | 0.491033033 |
| N,500 | 494 | (993/1000)*(1/999) | 0.000993994 | 0.491033033 |
| 100,N | 94 | (5/1000)*(993/999) | 0.00496997 | 0.467177177 |
| N,100 | 94 | (993/1000)*(5/999) | 0.00496997 | 0.467177177 |
| 100,(100) | 194 | (5/1000)*(4/999) | 2.002E-05 | 0.003883884 |
| N,N | -6 | (993/1000)*(992/999) | 0.986042042 | -5.916252252 |
| Total | 1 | -2 |
 Homework Sourse
Homework Sourse